【題目】在平面直角坐標系
中，已知橢圓
（
），圓
（
），若圓
的一條切線
與橢圓
相交于
兩點.
（1）當
， 
時，若點
都在坐標軸的正半軸上，求橢圓
的方程；
（2）若以
為直徑的圓經過坐標原點
，探究
是否滿足
，并說明理由.
【答案】（1）
（2）
【解析】試題分析：（1）利用點到直線的距離公式可求得
，由點
都在坐標軸的正半軸上，即可求得
和
的值，求得橢圓方程；（2）由以
為直徑的圓經過點
，可得
，即
，由
在直線
上，可將
用
表示，然后聯立直線與橢圓的方程結合韋達定理得
，化簡可得結論.
試題解析：（1）∵直線
與
相切，∴
.
由
， 
，解得
.
∵點
都在坐標軸正半軸上，
∴
.
∴切線
與坐標軸的交點為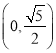
， 
.
∴
， 
.
∴橢圓
的方程是
.
（2）
的關系滿足
.
證明如下：設
， 
∵以
為直徑的圓經過點
，
∴
，即
.
∵點
在直線
上，
∴
.
∴
（*）
由
消去
，得
.
即
顯然
∴由一元二次方程根與系數的關系，得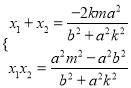
代入（*）式，得
.
整理，得
.
又由（1），有
.
消去
，得
∴
∴
滿足等量關系
.
第三學期贏在暑假系列答案
學練快車道快樂假期暑假作業新疆人民出版社系列答案科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐
中，底面
是直角梯形， 
， 
， 
， 
， 
是等邊三角形，且側面
底面
， 
分別是
， 
的中點.
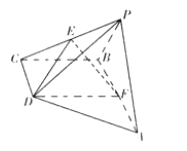
（Ⅰ）求證： 
平面
；
（Ⅱ）求平面
與平面
所成的二面角（銳角）的余弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校高三數學競賽初賽考試后，對部分考生的成績進行統計（考生成績均不低于90分，滿分150分），將成績按如下方式分成六組，若第四、五、六組的人數依次成等差數列，且第六組有4人．
（1）請補充完整頻率分布直方圖，并估計這組數據的平均數M；
（2）現根據初賽成績從第四組和第六組中任意選2人，記他們的成績分別為
.若
，則稱此二人為“黃金幫扶組”.試求選出的二人為“黃金幫扶組”的概率
；
（3）以此樣本的頻率當做概率，現隨機在這所有考生中選出3名學生，求成績不低于120分的人數
的分布列及期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，已知橢圓
（
），圓
（
），若圓
的一條切線
與橢圓
相交于
兩點.
（1）當
， 
時，若點
都在坐標軸的正半軸上，求橢圓
的方程；
（2）若以
為直徑的圓經過坐標原點
，探究
之間的等量關系，并說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】小明和爸爸媽媽、爺爺奶奶一同參加《中國詩詞大會》的現場錄制，5人坐成一排.若小 明的父母至少有一人與小明相鄰，則不同的坐法總數為________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知在平面直角坐標系中， 
是坐標原點，動圓
經過點
，且與直線
相切.
（1）求動圓圓心
的軌跡方程
；
（2）過
的直線
交曲線
于
兩點，過
作曲線
的切線
，直線
交于點
，求
的面積的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝|x－a|．
(1)若不等式f(x)≤3的解集為{x|－1≤x≤5}，求實數a的值；
(2)在(1)的條件下，若f(x)＋f(x＋5)≥m對一切實數x恒成立，求實數m的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
