
【題目】已知橢圓![]() 的焦點(diǎn)為
的焦點(diǎn)為![]() ,
,![]() ,離心率為
,離心率為![]() ,點(diǎn)P為橢圓C上一動點(diǎn),且
,點(diǎn)P為橢圓C上一動點(diǎn),且![]() 的面積最大值為
的面積最大值為![]() ,O為坐標(biāo)原點(diǎn).
,O為坐標(biāo)原點(diǎn).
(1)求橢圓C的方程;
(2)設(shè)點(diǎn)![]() ,
,![]() 為橢圓C上的兩個(gè)動點(diǎn),當(dāng)
為橢圓C上的兩個(gè)動點(diǎn),當(dāng)![]() 為多少時(shí),點(diǎn)O到直線MN的距離為定值.
為多少時(shí),點(diǎn)O到直線MN的距離為定值.
【答案】(1)![]() ;(2)當(dāng)
;(2)當(dāng)![]() =0時(shí),點(diǎn)O到直線MN的距離為定值
=0時(shí),點(diǎn)O到直線MN的距離為定值![]() .
.
【解析】
(1)![]() 的面積最大時(shí),
的面積最大時(shí),![]() 是短軸端點(diǎn),由此可得
是短軸端點(diǎn),由此可得![]() ,再由離心率及
,再由離心率及![]() 可得
可得![]() ,從而得橢圓方程;
,從而得橢圓方程;
(2)在直線![]() 斜率存在時(shí),設(shè)其方程為
斜率存在時(shí),設(shè)其方程為![]() ,現(xiàn)橢圓方程聯(lián)立消元(
,現(xiàn)橢圓方程聯(lián)立消元(![]() )后應(yīng)用韋達(dá)定理得
)后應(yīng)用韋達(dá)定理得![]() ,注意
,注意![]() ,一是計(jì)算
,一是計(jì)算![]() ,二是計(jì)算原點(diǎn)到直線
,二是計(jì)算原點(diǎn)到直線![]() 的距離,兩者比較可得結(jié)論.
的距離,兩者比較可得結(jié)論.
(1)因?yàn)?/span>![]() 在橢圓上,當(dāng)
在橢圓上,當(dāng)![]() 是短軸端點(diǎn)時(shí),
是短軸端點(diǎn)時(shí),![]() 到
到![]() 軸距離最大,此時(shí)
軸距離最大,此時(shí)![]() 面積最大,所以
面積最大,所以![]() ,由
,由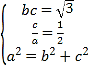 ,解得
,解得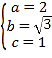 ,
,
所以橢圓方程為![]() .
.
(2)在![]() 時(shí),設(shè)直線
時(shí),設(shè)直線![]() 方程為
方程為![]() ,原點(diǎn)到此直線的距離為
,原點(diǎn)到此直線的距離為![]() ,即
,即![]() ,
,
由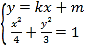 ,得
,得![]() ,
,
![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
![]()
![]() ,
,
所以當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() ,
,![]() 為常數(shù).
為常數(shù).
若![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
綜上所述,當(dāng)![]() =0時(shí),點(diǎn)O到直線MN的距離為定值
=0時(shí),點(diǎn)O到直線MN的距離為定值![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】湖南省會城市長沙又稱星城,是楚文明和湖湘文化的發(fā)源地,是國家首批歷史文化名城.城內(nèi)既有岳麓山、橘子洲等人文景觀,又有岳麓書院、馬王堆漢墓等名勝古跡,每年都有大量游客來長沙參觀旅游.為合理配置旅游資源,管理部門對首次來岳麓山景區(qū)游覽的游客進(jìn)行了問卷調(diào)查,據(jù)統(tǒng)計(jì),其中![]() 的人計(jì)劃只游覽岳麓山,另外
的人計(jì)劃只游覽岳麓山,另外![]() 的人計(jì)劃既游覽岳麓山又參觀馬王堆.每位游客若只游覽岳麓山,則記1分;若既游覽岳麓山又參觀馬王堆,則記2分.假設(shè)每位首次來岳麓山景區(qū)游覽的游客計(jì)劃是否參觀馬王堆相互獨(dú)立,視頻率為概率.
的人計(jì)劃既游覽岳麓山又參觀馬王堆.每位游客若只游覽岳麓山,則記1分;若既游覽岳麓山又參觀馬王堆,則記2分.假設(shè)每位首次來岳麓山景區(qū)游覽的游客計(jì)劃是否參觀馬王堆相互獨(dú)立,視頻率為概率.
(1)從游客中隨機(jī)抽取3人,記這3人的合計(jì)得分為![]() ,求
,求![]() 的分布列和數(shù)學(xué)期望;
的分布列和數(shù)學(xué)期望;
(2)從游客中隨機(jī)抽取![]() 人(
人(![]() ),記這
),記這![]() 人的合計(jì)得分恰為
人的合計(jì)得分恰為![]() 分的概率為
分的概率為![]() ,求
,求![]() ;
;
(3)從游客中隨機(jī)抽取若干人,記這些人的合計(jì)得分恰為![]() 分的概率為
分的概率為![]() ,隨著抽取人數(shù)的無限增加,
,隨著抽取人數(shù)的無限增加,![]() 是否趨近于某個(gè)常數(shù)?若是,求出這個(gè)常數(shù);若不是,說明理由.
是否趨近于某個(gè)常數(shù)?若是,求出這個(gè)常數(shù);若不是,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,正方形![]() 的邊長為
的邊長為![]() 為正三角形,平面
為正三角形,平面![]() 平面
平面![]() ,
,![]() 是線段
是線段![]() 的中點(diǎn),
的中點(diǎn),![]() 是線段
是線段![]() 上的動點(diǎn).
上的動點(diǎn).
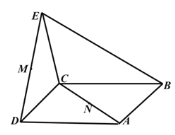
(1)探究![]() 四點(diǎn)共面時(shí),
四點(diǎn)共面時(shí),![]() 點(diǎn)位置,并證明;
點(diǎn)位置,并證明;
(2)當(dāng)![]() 四點(diǎn)共面時(shí),求
四點(diǎn)共面時(shí),求![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知在多面體![]() 中,平面
中,平面![]() 平面
平面![]() ,且四邊形
,且四邊形![]() 為正方形,且
為正方形,且![]() //
//![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點(diǎn).
的中點(diǎn).

(1)求證:![]() 平面
平面![]() ;
;
(2)求平面![]() 與平面
與平面![]() 所成的銳二面角的余弦值.
所成的銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
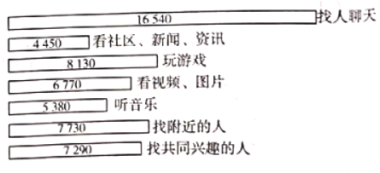
【題目】近年來,隨著![]() 網(wǎng)絡(luò)的普及和智能手機(jī)的更新?lián)Q代,各種方便的
網(wǎng)絡(luò)的普及和智能手機(jī)的更新?lián)Q代,各種方便的![]() 相繼出世,其功能也是五花八門.某大學(xué)為了調(diào)查在校大學(xué)生使用
相繼出世,其功能也是五花八門.某大學(xué)為了調(diào)查在校大學(xué)生使用![]() 的主要用途,隨機(jī)抽取了
的主要用途,隨機(jī)抽取了![]() 名大學(xué)生進(jìn)行調(diào)查,各主要用途與對應(yīng)人數(shù)的結(jié)果統(tǒng)計(jì)如圖所示,現(xiàn)有如下說法:
名大學(xué)生進(jìn)行調(diào)查,各主要用途與對應(yīng)人數(shù)的結(jié)果統(tǒng)計(jì)如圖所示,現(xiàn)有如下說法:
①可以估計(jì)使用![]() 主要聽音樂的大學(xué)生人數(shù)多于主要看社區(qū)、新聞、資訊的大學(xué)生人數(shù);
主要聽音樂的大學(xué)生人數(shù)多于主要看社區(qū)、新聞、資訊的大學(xué)生人數(shù);
②可以估計(jì)不足![]() 的大學(xué)生使用
的大學(xué)生使用![]() 主要玩游戲;
主要玩游戲;
③可以估計(jì)使用![]() 主要找人聊天的大學(xué)生超過總數(shù)的
主要找人聊天的大學(xué)生超過總數(shù)的![]() .
.
其中正確的個(gè)數(shù)為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖1,四邊形![]() 為直角梯形,
為直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為線段
為線段![]() 上一點(diǎn),滿足
上一點(diǎn),滿足![]() ,
,![]() 為
為![]() 的中點(diǎn),現(xiàn)將梯形沿
的中點(diǎn),現(xiàn)將梯形沿![]() 折疊(如圖2),使平面
折疊(如圖2),使平面![]() 平面
平面![]() .
.
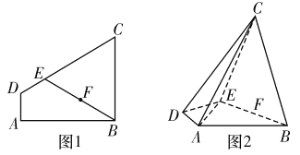
(1)求證:平面![]() 平面
平面![]() ;
;
(2)能否在線段![]() 上找到一點(diǎn)
上找到一點(diǎn)![]() (端點(diǎn)除外)使得直線
(端點(diǎn)除外)使得直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ?若存在,試確定點(diǎn)
?若存在,試確定點(diǎn)![]() 的位置;若不存在,請說明理由.
的位置;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知正項(xiàng)等比數(shù)列{an}滿足a1=2,2a2=a4﹣a3,數(shù)列{bn}滿足bn=1+2log2an.
(1)求數(shù)列{an},{bn}的通項(xiàng)公式;
(2)令cn=anbn,求數(shù)列{cn}的前n項(xiàng)和Sn;
(3)若λ>0,且對所有的正整數(shù)n都有2λ2﹣kλ+2![]() 成立,求k的取值范圍.
成立,求k的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 的各項(xiàng)均為正數(shù),記數(shù)列
的各項(xiàng)均為正數(shù),記數(shù)列![]() 的前n項(xiàng)和為
的前n項(xiàng)和為![]() ,數(shù)列
,數(shù)列![]() 的前n項(xiàng)和為
的前n項(xiàng)和為![]() ,且
,且![]() .
.
(1)求![]() 的值;
的值;
(2)求數(shù)列![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(3)若![]() ,且
,且![]() 成等比數(shù)列,求k和t的值.
成等比數(shù)列,求k和t的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() 上一點(diǎn)
上一點(diǎn)![]() ,F為焦點(diǎn),
,F為焦點(diǎn),![]() 面積為1.
面積為1.
(1)求拋物線C的方程;
(2)過點(diǎn)P引圓![]() 的兩條切線PA、PB,切線PA、PB與拋物線C的另一個(gè)交點(diǎn)分別為A、B,求直線AB斜率的取值范圍.
的兩條切線PA、PB,切線PA、PB與拋物線C的另一個(gè)交點(diǎn)分別為A、B,求直線AB斜率的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com