
【題目】已知函數![]() (其中
(其中![]() ).
).
(1)當![]() 時,求函數
時,求函數![]() 的圖像在
的圖像在![]() 處的切線方程;
處的切線方程;
(2)若![]() 恒成立,求
恒成立,求![]() 的取值范圍;
的取值范圍;
(3)設![]() ,且函數
,且函數![]() 有極大值點
有極大值點![]() ,求證:
,求證: ![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)見解析。
;(3)見解析。
【解析】試題分析:
(1)根據導數的幾何意義可得所求的切線方程.(2)由題意分離參數可得![]() 在
在![]() 上恒成立,設
上恒成立,設![]() ,利用導數可求得
,利用導數可求得![]() ,故
,故![]() ,解得
,解得![]() ,即為所求范圍.(3)將
,即為所求范圍.(3)將![]() 求導后由
求導后由![]() 及根與系數的關系可得極大值點
及根與系數的關系可得極大值點![]() ,然后得到
,然后得到![]() ,
, ![]() .設
.設![]() ,求導可得
,求導可得![]() 在
在![]() 上單調遞減,故
上單調遞減,故![]() ,即不等式成立.
,即不等式成立.
試題解析:
(1)當![]() 時,
時, ![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
又![]() ,
,
∴所求的切線方程為![]() ,
,
即![]()
(2)有題意得![]() 在
在![]() 上恒成立,
上恒成立,
∴![]() 在
在![]() 上恒成立,
上恒成立,
∵![]() ,
,
∴![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,則
,則![]()
∴當![]() 時,
時, ![]() ,
, ![]() 單調遞增;
單調遞增;
當![]() 時,
時, ![]() ,
, ![]() 單調遞減.
單調遞減.
∴當![]() 時,
時, ![]() 取得極大值,也為最大值,且
取得極大值,也為最大值,且![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴實數![]() 的取值范圍是
的取值范圍是![]() .
.
(3)證明:由題意得![]() ,
, ![]() ,
,
∴![]() ,
,
①當![]() 時,
時, ![]() ,
, ![]() 單調遞增,無極值點.不符合題意;
單調遞增,無極值點.不符合題意;
②當![]() 或
或![]() 時,設
時,設![]() 的兩根為
的兩根為![]() 和
和![]() ,
,
∵![]() 為函數
為函數![]() 的極大值點,
的極大值點,
∴![]() ,
,
由![]() ,
, ![]() ,知
,知![]() ,
, ![]() ,
,
又由![]() ,得
,得![]() ,
,
∵![]() ,
, ![]() ,
,
令![]() ,
,
則![]() ,
,
令![]() ,
, ![]() ,
,
則![]() ,
,
∴當![]() 時,
時, ![]() ,
, ![]() 單調遞增;
單調遞增;
當![]() 時,
時, ![]() ,
, ![]() 單調遞減.
單調遞減.
∴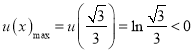 ,
,
∴![]()
∴![]() 在
在![]() 上單調遞減,
上單調遞減,
∴![]() ,
,
∴![]() .
.


科目:高中數學 來源: 題型:
【題目】4男3女站成一排,求滿足下列條件的排法共有多少種?
![]() 任何兩名女生都不相鄰,有多少種排法?
任何兩名女生都不相鄰,有多少種排法?
![]() 男甲不在首位,男乙不在末位,有多少種排法?
男甲不在首位,男乙不在末位,有多少種排法?
![]() 男生甲、乙、丙順序一定,有多少種排法?
男生甲、乙、丙順序一定,有多少種排法?
![]() 男甲在男乙的左邊
男甲在男乙的左邊![]() 不一定相鄰
不一定相鄰![]() 有多少種不同的排法?
有多少種不同的排法?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 中點(如圖1).將
中點(如圖1).將![]() 沿
沿![]() 折起到圖2中
折起到圖2中![]() 的位置,得到四棱錐
的位置,得到四棱錐![]() .
.
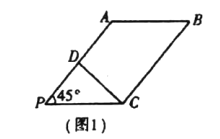
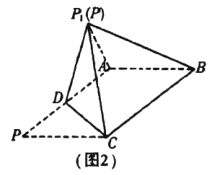
(1)將![]() 沿
沿![]() 折起的過程中,
折起的過程中, ![]() 平面
平面![]() 是否成立?并證明你的結論;
是否成立?并證明你的結論;
(2)若![]() 與平面
與平面![]() 所成的角為60°,且
所成的角為60°,且![]() 為銳角三角形,求平面
為銳角三角形,求平面![]() 和平面
和平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動圓過定點![]() ,且在y軸上截得的弦MN的長為4.
,且在y軸上截得的弦MN的長為4.
(1)求動圓圓心的軌跡C的方程;
(2)過點![]() 的直線
的直線![]() 與曲線C交于A、B兩點,線段AB的垂直平分線與x軸交于點E(
與曲線C交于A、B兩點,線段AB的垂直平分線與x軸交于點E(![]() ,0),求
,0),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}滿足:a3=7,a5+a7=26,{an}的前n項和為Sn.
(1)求an及Sn;
(2)令bn=![]() (n∈N*),求數列{bn}的前n項和Tn.
(n∈N*),求數列{bn}的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有![]() 六支足球隊參加單循環比賽(即任意兩支球隊只踢一場比賽),第一周的比賽中
六支足球隊參加單循環比賽(即任意兩支球隊只踢一場比賽),第一周的比賽中![]() ,各踢了
,各踢了![]() 場,
場, ![]() 各踢了
各踢了![]() 場,
場, ![]() 踢了
踢了![]() 場,且
場,且![]() 隊與
隊與![]() 隊未踢過,
隊未踢過, ![]() 隊與
隊與![]() 隊也未踢過,則在第一周的比賽中,
隊也未踢過,則在第一周的比賽中, ![]() 隊踢的比賽的場數是( )
隊踢的比賽的場數是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2016年“雙節”期間,高速公路車輛較多.某調查公司在一服務區從七座以下小型汽車中按進服務區的先后每間隔50輛就抽取一輛的抽樣方法抽取40名駕駛員進行詢問調查,將他們在某段高速公路的車速![]() 分成六段:
分成六段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 后得到如圖的頻率分布直方圖.
后得到如圖的頻率分布直方圖.
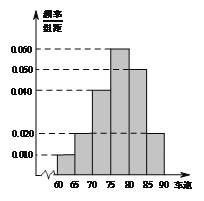
(I)某調查公司在采樣中,用到的是什么抽樣方法?
(II)求這40輛小型車輛車速的眾數、中位數及平均數的估計值;
(III)若從車速在![]() 的車輛中任抽取2輛,求車速在
的車輛中任抽取2輛,求車速在![]() 的車輛至少有一輛的概率.
的車輛至少有一輛的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
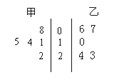
【題目】某校高中年級開設了豐富多彩的校本課程,甲、乙兩班各隨機抽取了5名學生的學分,用莖葉圖表示.![]() ,
,![]() 分別表示甲、乙兩班各自5名學生學分的標準差,則
分別表示甲、乙兩班各自5名學生學分的標準差,則![]() _______
_______![]() .(填“
.(填“![]() ”“<”或“=”)
”“<”或“=”)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】質監部門從某超市銷售的甲、乙兩種食用油中分別各隨機抽取100桶檢測某項質量指標,由檢測結果得到如下的頻率分布直方圖:
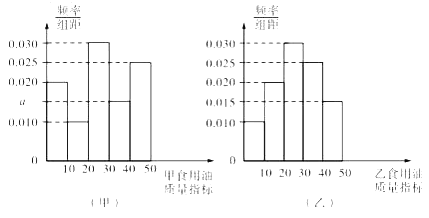
(Ⅰ)寫出頻率分布直方圖(甲)中![]() 的值;記甲、乙兩種食用油100桶樣本的質量指標的方差分別為
的值;記甲、乙兩種食用油100桶樣本的質量指標的方差分別為![]() ,
,![]() ,試比較
,試比較![]() ,
,![]() 的大小(只要求寫出答案);
的大小(只要求寫出答案);
(Ⅱ)估計在甲、乙兩種食用油中隨機抽取1捅,恰有一桶的質量指標大于20;
(Ⅲ)由頻率分布直方圖可以認為,乙種食用油的質量指標值![]() 服從正態分布
服從正態分布![]() .其中
.其中![]() 近似為樣本平均數
近似為樣本平均數![]() ,
,![]() 近似為樣本方差
近似為樣本方差![]() ,設
,設![]() 表示從乙種食用油中隨機抽取10桶,其質量指標值位于(14.55,38.45)的桶數,求
表示從乙種食用油中隨機抽取10桶,其質量指標值位于(14.55,38.45)的桶數,求![]() 的數學期望.
的數學期望.
注:①同一組數據用該區問的中點值作代表,計算得![]()
②若![]()
![]() ,則
,則![]() ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com