
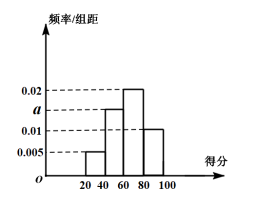
【題目】某校為了解校園安全教育系列活動的成效,對全校學生進行了一次安全意識測試,根據測試成績評定“合格”“不合格”兩個等級,同時對相應等級進行量化:“合格”記5分,“不合格”記0分.現隨機抽取部分學生的答卷,統計結果及對應的頻率分布直方圖如下:
等級 | 不合格 | 合格 | ||
得分 |
|
|
|
|
頻數 | 6 | a | 24 | b |
(1)由該題中頻率分布直方圖求測試成績的平均數和中位數;
(2)其他條件不變在評定等級為“合格”的學生中依次抽取2人進行座談,每次抽取1人,求在第1次抽取的測試得分低于80分的前提下,第2次抽取的測試得分仍低于80分的概率;
(3)用分層抽樣的方法,從評定等級為“合格”和“不合格”的學生中抽取10人進行座談.現再從這10人中任選4人,記所選4人的量化總分為![]() ,求
,求![]() 的數學期望
的數學期望![]() .
.
【答案】(1)64,65;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先求出![]() 的值,再利用頻率分布直方圖平均數和中位數的公式求解;
的值,再利用頻率分布直方圖平均數和中位數的公式求解;
(2)“第1次抽取的測試得分低于80分”為事件A,“第2次抽取的測試得分低于80分”為事件B,再利用條件概率求解;
(3)由題意可得![]() 的所有可能取值為0,5,10,15,20,再求出其對應的概率,即得
的所有可能取值為0,5,10,15,20,再求出其對應的概率,即得![]() 的分布列和數學期望
的分布列和數學期望![]() .
.
由題意知,樣本容量為![]() ,
,![]() ,
,
![]() ,
,![]() .
.
(1)平均數為![]() ,
,
設中位數為x,
因為![]()
![]() ,
,![]() ,
,
所以![]() ,則
,則![]() ,
,
解得![]() .
.
(2)由題意可知,分數在![]() 內的學生有24人,分數在
內的學生有24人,分數在![]() 內的學生有12人.設“第1次抽取的測試得分低于80分”為事件A,“第2次抽取的測試得分低于80分”為事件B,
內的學生有12人.設“第1次抽取的測試得分低于80分”為事件A,“第2次抽取的測試得分低于80分”為事件B,
則![]() ,
,![]() ,所以
,所以![]() .
.
(3)在評定等級為“合格”和“不合格”的學生中用分層抽樣的方法抽取10人,則“不合格”的學生人數為![]() ,“合格”的學生人數為
,“合格”的學生人數為![]() .
.
由題意可得![]() 的所有可能取值為0,5,10,15,20
的所有可能取值為0,5,10,15,20
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
所以![]() 的分布列為
的分布列為
| 0 | 5 | 10 | 15 | 20 |
P |
|
|
|
|
|
![]() .
.


 輕松奪冠全能掌控卷系列答案
輕松奪冠全能掌控卷系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上.
上.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設![]() 為原點,過原點的直線(不與
為原點,過原點的直線(不與![]() 軸垂直)與橢圓
軸垂直)與橢圓![]() 交于
交于![]() 、
、![]() 兩點,直線
兩點,直線![]() 、
、![]() 與
與![]() 軸分別交于點
軸分別交于點![]() 、
、![]() .問:
.問:![]() 軸上是否存在定點
軸上是否存在定點![]() ,使得
,使得![]() ?若存在,求點
?若存在,求點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數學中有許多形狀優美、寓意美好的曲線,如下圖就是在平面直角坐標系的“心形曲線”,又名RC心形線.如果以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系,其RC心形線的極坐標方程為
軸正半軸為極軸,建立極坐標系,其RC心形線的極坐標方程為![]() .
.
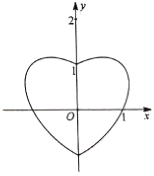
(1)求RC心形線的直角坐標方程;
(2)已知![]() 與直線
與直線![]() (
(![]() 為參數),若直線
為參數),若直線![]() 與RC心形線交于兩點
與RC心形線交于兩點![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國農業銀行廣元分行發行“金穗廣元·劍門關旅游卡”是以“游廣元、知廣元、愛廣元共享和諧廣元”為主題活動的一項經濟性和公益性相結合的重大舉措,以最優惠的價格惠及廣元戶籍市民、浙江及黑龍江授建省群眾、省內援建市市民,凡上述對象均可辦理此卡,本人憑此卡及本人身份證一年內(期滿后可重新充值辦理)在廣元市范圍內可無限次游覽所有售門票景區景點,如:劍門關、朝天明月峽、旺蒼鼓城山—七里峽、青川唐家河、廣元皇澤寺、蒼溪梨博園、昭化古城等,現有浙江及黑龍江援建省群眾甲乙兩人到廣元旅游(同游),第一天他們游覽了劍門關、朝天明月峽,第二天他們準備從上面剩下的5個景點中選兩個景點游覽,則第二天游覽青川唐家河的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圖1是由邊長為4的正六邊形![]() ,矩形
,矩形![]() ,組成的一個平面圖形,將其沿
,組成的一個平面圖形,將其沿![]() ,
,![]() 折起得幾何體
折起得幾何體![]() ,使得
,使得![]() ,且平面
,且平面![]() 平面
平面![]() ,如圖2.
,如圖2.
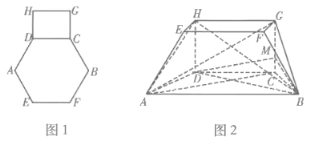
(1)證明:圖2中,平面![]() 平面
平面![]() ;
;
(2)設點M為圖2中線段![]() 上一點,且
上一點,且![]() ,若直線
,若直線![]() 平面
平面![]() ,求圖2中的直線
,求圖2中的直線![]() 與平面
與平面![]() 所成角的正弦值
所成角的正弦值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過拋物線C:x2=4y的準線上任意一點P作拋物線的切線PA,PB,切點分別為A,B,則A點到準線的距離與B點到準線的距離之和的最小值是( )
A.7B.6C.5D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】新生兒某疾病要接種三次疫苗免疫(即0、1、6月齡),假設每次接種之間互不影響,每人每次接種成功的概率相等為了解新生兒該疾病疫苗接種劑量與接種成功之間的關系,現進行了兩種接種方案的臨床試驗:10μg/次劑量組與20μg/次劑量組,試驗結果如下:
接種成功 | 接種不成功 | 總計(人) | |
10μg/次劑量組 | 900 | 100 | 1000 |
20μg/次劑量組 | 973 | 27 | 1000 |
總計(人) | 1873 | 127 | 2000 |
(1)根據數據說明哪種方案接種效果好?并判斷能否有99.9%的把握認為該疾病疫苗接種成功與兩種接種方案有關?
(2)以頻率代替概率,若選用接種效果好的方案,參與該試驗的1000人的成功人數比此劑量只接種一次的成功人數平均提高多少人.
參考公式: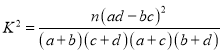 ,其中
,其中![]()
參考附表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
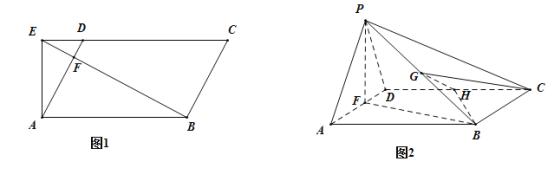
【題目】在平行四邊形![]() 中,
中,![]() 過
過![]() 點作
點作![]() 的垂線交
的垂線交![]() 的延長線于點
的延長線于點![]() ,
,![]() .連結
.連結![]() 交
交![]() 于點
于點![]() ,如圖1,將
,如圖1,將![]() 沿
沿![]() 折起,使得點
折起,使得點![]() 到達點
到達點![]() 的位置.如圖2.
的位置.如圖2.
![]() 證明:直線
證明:直線![]()
![]() 平面
平面![]()
![]() 若
若![]() 為
為![]() 的中點,
的中點,![]() 為
為![]() 的中點,且平面
的中點,且平面![]() 平面
平面![]() 求三棱錐
求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com