
【題目】某公司為了確定下一年度投入某種產品的宣傳費用,需了解年宣傳費x(單位:萬元)對年銷量y(單位:噸)和年利潤(單位:萬元)的影響.對近6宣傳費xi和年銷售量yi(i=1,2,3,4,5,6)的數據做了初步統計,得到如下數據:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年宣傳費x(萬元) | 38 | 48 | 58 | 68 | 78 | 88 |
年銷售量y(噸) | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
經電腦模擬,發現年宣傳費x(萬元)與年銷售量y(噸)之間近似滿足關系式y=axb(a,b>0),即lny=blnx+lna.,對上述數據作了初步處理,得到相關的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(Ⅰ)從表中所給出的6年年銷售量數據中任選2年做年銷售量的調研,求所選數據中至多有一年年銷售量低于20噸的概率.
(Ⅱ)根據所給數據,求![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(Ⅲ) 若生產該產品的固定成本為200(萬元),且每生產1(噸)產品的生產成本為20(萬元)(總成本=固定成本+生產成本+年宣傳費),銷售收入為![]() (萬元),假定該產品產銷平衡(即生產的產品都能賣掉),則2019年該公司應該投入多少宣傳費才能使利潤最大?(其中
(萬元),假定該產品產銷平衡(即生產的產品都能賣掉),則2019年該公司應該投入多少宣傳費才能使利潤最大?(其中![]() )
)
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 中的斜率和截距的最小二乘估計分別為
中的斜率和截距的最小二乘估計分別為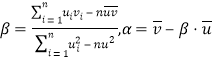
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() (Ⅲ)100萬元
(Ⅲ)100萬元
【解析】
(Ⅰ)利用古典概型計算公式即可得到結果;
(Ⅱ)分別求出u,v的平均數,求出相關系數求出回歸方程即可;
(Ⅲ)設該公司的年利潤為![]() ,因為利潤=銷售收入-總成本,根據二次函數的圖象與性質求最值即可.
,因為利潤=銷售收入-總成本,根據二次函數的圖象與性質求最值即可.
解:(Ⅰ)記事件![]() 表示“至多有一年年銷量低于20噸”,由表中數據可知6年的數據中有2013年和2014年的年銷量低于20噸,記這兩年為
表示“至多有一年年銷量低于20噸”,由表中數據可知6年的數據中有2013年和2014年的年銷量低于20噸,記這兩年為![]() ,其余四年為
,其余四年為![]() ,則從6年中任取2年共有
,則從6年中任取2年共有![]() ,
,![]() 15種不同取法,
15種不同取法,
事件![]() 包括
包括![]() ,
,![]() 共14種取法,故
共14種取法,故![]()
(Ⅱ)對![]() 兩邊取對數得
兩邊取對數得![]() ,令
,令![]() 得
得![]() ,由題中數據得:
,由題中數據得:![]() ,
,![]()
![]() ,
,![]()
所以 ,由
,由![]() ,得
,得![]() ,
,
故所求回歸方程為![]()
(Ⅲ)設該公司的年利潤為![]() ,因為利潤=銷售收入-總成本,所以由題意可知
,因為利潤=銷售收入-總成本,所以由題意可知
![]() ,
,
所以當![]() 即
即![]() 時,利潤
時,利潤![]() 取得最大值500(萬元),故2019年該公司投入100萬元的宣傳費才能獲得最大利潤.
取得最大值500(萬元),故2019年該公司投入100萬元的宣傳費才能獲得最大利潤.


 陽光課堂課時作業系列答案
陽光課堂課時作業系列答案科目:高中數學 來源: 題型:
【題目】自出生之日起,人的情緒、體力、智力等心理、生理狀況就呈周期變化,變化由線為![]() .根據心理學家的統計,人體節律分為體力節律、情緒節律和智力節律三種.這些節律的時間周期分別為23天、28天、33天.每個節律周期又分為高潮期、臨界日和低潮期三個階段.以上三個節律周期的半數為臨界日,這就是說11.5天、14天、16.5天分別為體力節律、情緒節律和智力節律的臨界日.臨界日的前半期為高潮期,后半期為低潮期.生日前一天是起始位置(平衡位置),已知小英的生日是2003年3月20日(每年按365天計算).
.根據心理學家的統計,人體節律分為體力節律、情緒節律和智力節律三種.這些節律的時間周期分別為23天、28天、33天.每個節律周期又分為高潮期、臨界日和低潮期三個階段.以上三個節律周期的半數為臨界日,這就是說11.5天、14天、16.5天分別為體力節律、情緒節律和智力節律的臨界日.臨界日的前半期為高潮期,后半期為低潮期.生日前一天是起始位置(平衡位置),已知小英的生日是2003年3月20日(每年按365天計算).
(1)請寫出小英的體力、情緒和智力節律曲線的函數;
(2)試判斷小英在2019年4月22日三種節律各處于什么階段,當日小英是否適合參加某項體育競技比賽?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】墻上有一壁畫,最高點![]() 處離地面
處離地面![]() 米,最低點
米,最低點![]() 處離地面
處離地面![]() 米,距離墻
米,距離墻![]() 米處設有防護欄,觀察者從離地面高
米處設有防護欄,觀察者從離地面高![]() 米的
米的![]() 處觀賞它.
處觀賞它.
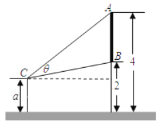
(1)當![]() 時,觀察者離墻多遠時,視角
時,觀察者離墻多遠時,視角![]() 最大?
最大?
(2)若![]() ,視角
,視角![]() 的正切值恒為
的正切值恒為![]() ,觀察者離墻的距離應在什么范圍內?
,觀察者離墻的距離應在什么范圍內?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中
,其中![]() 為自然對數的底數.
為自然對數的底數.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)寫出函數![]() 的單調遞減區間(無需證明) ;
的單調遞減區間(無需證明) ;
(Ⅲ)若實數![]() 滿足
滿足![]() ,則稱
,則稱![]() 為
為![]() 的二階不動點,求函數
的二階不動點,求函數![]() 的二階不動點的個數.
的二階不動點的個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的幾何體是圓柱的一部分,它是由矩形![]() (及其內部)以
(及其內部)以![]() 邊所在直線為旋轉軸旋轉
邊所在直線為旋轉軸旋轉![]() 得到的,點
得到的,點![]() 是弧
是弧![]() 上的一點,點
上的一點,點![]() 是弧
是弧![]() 的中點.
的中點.
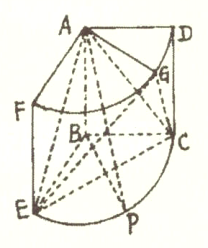
(1)求證:平面![]() 平面
平面![]() ;
;
(2)當![]() 且
且![]() 時,求二面角
時,求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調查觀眾對某熱播電視劇的喜愛程度,某電視臺在甲、乙兩地各隨機抽取了8名觀眾作問卷調查,得分統計結果如圖所示:
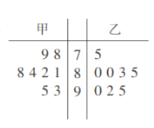
(1)計算甲、乙兩地被抽取的觀眾問卷的平均得分;
(2)計算甲、乙兩地被抽取的觀眾問卷得分的方差;
(3)若從甲地被抽取的8名觀眾中再邀請2名進行深入調研,求這2名觀眾中恰有1人的問卷調查成績在90分以上的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲廠根據以往的生產銷售經驗得到下面有關生產銷售的統計規律:每生產產品![]() (百臺),其總成本為
(百臺),其總成本為![]() (萬元),其中固定成本為2.8萬元,并且每生產1百臺的生產成本為1萬元(總成本=固定成本+生產成本),銷售收入
(萬元),其中固定成本為2.8萬元,并且每生產1百臺的生產成本為1萬元(總成本=固定成本+生產成本),銷售收入![]() (萬元)滿足
(萬元)滿足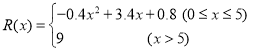 ,假定該產品產銷平衡(即生產的產品都能賣掉),根據上述統計規律,完成下列問題:
,假定該產品產銷平衡(即生產的產品都能賣掉),根據上述統計規律,完成下列問題:
(1)寫出利潤函數![]() 的解析式(利潤=銷售收入-總成本);
的解析式(利潤=銷售收入-總成本);
(2)甲廠生產多少臺產品時,可使盈利最多?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=![]() ,x∈(-2,2).
,x∈(-2,2).
(1) 判斷f(x)的奇偶性并說明理由;
(2) 求證:函數f(x)在(-2,2)上是增函數;
(3) 若f(2+a)+f(1-2a)>0,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,定義:
,定義:![]() 表示不小于
表示不小于![]() 的最小整數,例如:
的最小整數,例如:![]() ,
,![]() .
.
(1)若![]() ,求實數
,求實數![]() 的取值范圍;
的取值范圍;
(2)若![]() ,求
,求![]() 時實數
時實數![]() 的取值范圍;
的取值范圍;
(3)設![]() ,
,![]() ,若對于任意的
,若對于任意的![]() ,都有
,都有![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com