
【題目】設函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 的最大值;
的最大值;
(2)令![]() ,其圖象上存在一點
,其圖象上存在一點![]() ,使此處切線的斜率
,使此處切線的斜率![]() ,求實數
,求實數![]() 的取值范圍;
的取值范圍;
(3)當![]() ,
, ![]() 時,方程
時,方程![]() 有唯一實數解,求正數
有唯一實數解,求正數![]() 的值.
的值.
【答案】(1) ![]() (2)
(2) ![]() (3)
(3)![]()
【解析】試題分析:(1)依題意確定![]() 的定義域,對
的定義域,對![]() 求導,求出函數的單調性,即可求出函數
求導,求出函數的單調性,即可求出函數![]() 的最大值;(2)表示出
的最大值;(2)表示出![]() ,根據其圖象上存在一點
,根據其圖象上存在一點![]() ,使此處切線的斜率
,使此處切線的斜率![]() 可得
可得![]() ,在
,在![]() 上有解,即可求出實數
上有解,即可求出實數![]() 的取值范圍;(3)由
的取值范圍;(3)由![]() ,方程
,方程![]() 有唯一實數解,構造函數
有唯一實數解,構造函數![]() ,求出
,求出![]() 的單調性,即可求出正數
的單調性,即可求出正數![]() 的值.
的值.
試題解析:(1)依題意, ![]() 的定義域為
的定義域為![]() ,當
,當![]() 時,
時, ![]() ,
, ![]()
由![]() ,得
,得![]() ,解得
,解得![]()
由![]() ,得
,得![]() ,解得
,解得![]() 或
或![]()
∵![]() ,∴
,∴![]() 在
在![]() 單調遞増,在
單調遞増,在![]() 單調遞減;所以
單調遞減;所以![]() 的極大值為
的極大值為![]() ,此即為最大值
,此即為最大值
(2)![]() ,則有
,則有![]() ,在
,在![]() 上有解,
上有解,
∴![]() ,
, ![]() ,∵
,∵![]() ,所以當
,所以當![]() 時,
時, ![]()
取得最小值![]() ,∴
,∴![]()
(3)由![]() 得
得![]() ,令
,令![]() ,
, 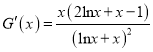
令![]() ,
, ![]() ,∴
,∴![]() 在
在![]() 上單調遞增,而
上單調遞增,而![]() ,
,
∴在![]() ,即
,即![]() ,在
,在![]() ,即
,即![]() ,
,
∴![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 單調遞増,∴
單調遞増,∴![]() 極小值
極小值![]() ,令
,令![]() ,即
,即![]() 時方程
時方程![]() 有唯一實數解.
有唯一實數解.


科目:高中數學 來源: 題型:
【題目】某P2P平臺需要了解該平臺投資者的大致年齡分布,發現其投資者年齡大多集中在區間[20,50]歲之間,對區間[20,50]歲的人群隨機抽取20人進行了一次理財習慣調查,得到如下統計表和各年齡段人數頻率分布直方圖:
組數 | 分組 | 人數(單位:人) |
第一組 | [20,25) | 2 |
第二組 | [25,30) | a |
第三組 | [30,35) | 5 |
第四組 | [35,40) | 4 |
第五組 | [40,45) | 3 |
第六組 | [45,50] | 2 |

(Ⅰ)求a的值并畫出頻率分布直方圖;
(Ⅱ)在統計表的第五與第六組的5人中,隨機選取2人,求這2人的年齡都小于45歲的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某海輪以每小時30海里的速度航行,在點![]() 測得海面上油井
測得海面上油井![]() 在南偏東
在南偏東![]() ,海輪向北航行40分鐘后到達點
,海輪向北航行40分鐘后到達點![]() ,測得油井
,測得油井![]() 在南偏東
在南偏東![]() ,海輪改為北偏東
,海輪改為北偏東![]() 的航向再行駛80分鐘到達點
的航向再行駛80分鐘到達點![]() ,則
,則![]() 兩點的距離為(單位:海里)
兩點的距離為(單位:海里)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】大西洋鮭魚每年都要逆流而上,游回產地產卵,經研究發現鮭魚的游速可以表示為函數y=![]() log3(
log3(![]() ),單位是m/s,θ是表示魚的耗氧量的單位數.
),單位是m/s,θ是表示魚的耗氧量的單位數.
(1)當一條鮭魚的耗氧量是900個單位時,它的游速是多少?
(2)計算一條魚靜止時耗氧量的單位數。
(3)某條鮭魚想把游速提高1 m/s,那么它的耗氧量的單位數是原來的多少倍?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)對任意的m,n∈R都有f(m+n)=f(m)+f(n)-1,并且x>0時,恒有f(x)>1.
(1)求證:f(x)在R上是增函數;
(2)若f(3)=4,解不等式f(a2+a-5)<2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位建造一間地面面積為12![]() 的背面靠墻的矩形小房,由于地理位置的限制,房子側面的長度
的背面靠墻的矩形小房,由于地理位置的限制,房子側面的長度![]() 不得超過
不得超過![]() 米,房屋正面的造價為400元/
米,房屋正面的造價為400元/![]() ,房屋側面的造價為150元/
,房屋側面的造價為150元/![]() ,屋頂和地面的造價費用合計為5800元,如果墻高為3
,屋頂和地面的造價費用合計為5800元,如果墻高為3![]() ,且不計房屋背面的費用.
,且不計房屋背面的費用.
(1)把房屋總價![]() 表示成
表示成![]() 的函數,并寫出該函數的定義域;
的函數,并寫出該函數的定義域;
(2)當側面的長度為多少時,總造價最低?最低總造價是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于在區間![]() 上有意義的函數
上有意義的函數![]() ,滿足對任意的
,滿足對任意的![]() ,
,![]() ,有
,有![]() 恒成立,厄稱
恒成立,厄稱![]() 在
在![]() 上是“友好”的,否則就稱
上是“友好”的,否則就稱![]() 在
在![]() 上是“不友好”的,現有函數
上是“不友好”的,現有函數![]() .
.
(1)若函數![]() 在區間
在區間![]() (
(![]() )上是“友好”的,求實數
)上是“友好”的,求實數![]() 的取值范圍;
的取值范圍;
(2)若關于![]() 的方程
的方程![]() 的解集中有且只有一個元素,求實數
的解集中有且只有一個元素,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com