
【題目】《數(shù)書九章》是中國南宋時期杰出數(shù)學家秦九韶的著作,其中在卷五“三斜求積”中提出了已知三角形三邊![]() 、
、![]() 、
、![]() ,求面積的公式,這與古希臘的海倫公式完全等價,其求法是“以小斜冥并大斜冥減中斜冥,余半之,自乘于上,以小斜冥乘大斜冥減上,余四約之,為實.一為從隅,開平方得積”若把以上這段文字寫出公式,即若
,求面積的公式,這與古希臘的海倫公式完全等價,其求法是“以小斜冥并大斜冥減中斜冥,余半之,自乘于上,以小斜冥乘大斜冥減上,余四約之,為實.一為從隅,開平方得積”若把以上這段文字寫出公式,即若![]() ,則
,則![]() .
.
(1)已知![]() 的三邊
的三邊![]() ,
,![]() ,
,![]() ,且
,且![]() ,求證:
,求證:![]() 的面積
的面積![]() .
.
(2)若![]() ,
,![]() ,求
,求![]() 的面積
的面積![]() 的最大值.
的最大值.
科目:高中數(shù)學 來源: 題型:
【題目】已知兩點![]() 、
、![]() ,動點
,動點![]() 在
在![]() 軸上的射影是
軸上的射影是![]() ,且
,且![]() .
.
(1)求動點![]() 的軌跡方程;
的軌跡方程;
(2)設直線![]() 、
、![]() 的兩個斜率存在,分別記為
的兩個斜率存在,分別記為![]() 、
、![]() ,若
,若![]() ,求點
,求點![]() 的坐標;
的坐標;
(3)若經(jīng)過點![]() 的直線
的直線![]() 與動點
與動點![]() 的軌跡有兩個交點
的軌跡有兩個交點![]() 、
、![]() ,當
,當![]() 時,求直線
時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】學生人均課外學習時間是指單日內學生不在教室內的平均學習時間,這種課外學習時間對學生的學習有一定的影響.合肥市經(jīng)開區(qū)某著名高中學生群體![]() 有走讀生和住校生兩種,調查顯示:當群體
有走讀生和住校生兩種,調查顯示:當群體![]() 中
中![]() 的學生為走讀生時,走讀生的人均課外學習時間(單位分鐘)為
的學生為走讀生時,走讀生的人均課外學習時間(單位分鐘)為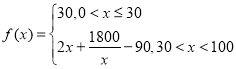 ,而住校生的人均課外學習時間恒為40分鐘,試根據(jù)上述調查結果回答下列問題:
,而住校生的人均課外學習時間恒為40分鐘,試根據(jù)上述調查結果回答下列問題:
(1)當![]() 為何值時,住校生的人均課外學習時間等于走讀生的課外人均學習時間?
為何值時,住校生的人均課外學習時間等于走讀生的課外人均學習時間?
(2)求該校高中學生群體![]() 的人均課外學習時間
的人均課外學習時間![]() 的表達式,并求
的表達式,并求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知定義在![]() 上的偶函數(shù)
上的偶函數(shù)![]() 和奇函數(shù)
和奇函數(shù)![]() ,且
,且![]() .
.
(1)求函數(shù)![]() ,
,![]() 的解析式;
的解析式;
(2)設函數(shù) ,記
,記![]() (
(![]() ,
,![]() ).探究是否存在正整數(shù)
).探究是否存在正整數(shù)![]() ,使得對任意的
,使得對任意的![]() ,不等式
,不等式![]() 恒成立?若存在,求出所有滿足條件的正整數(shù)
恒成立?若存在,求出所有滿足條件的正整數(shù)![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
參考結論:設![]() 均為常數(shù),函數(shù)
均為常數(shù),函數(shù)![]() 的圖象關于點
的圖象關于點![]() 對稱的充要條件是
對稱的充要條件是![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,其中a,
,其中a,![]() .
.
(1)當![]() ,
,![]() 時,求函數(shù)
時,求函數(shù)![]() 的零點;
的零點;
(2)當![]() 時,解關于x的不等式
時,解關于x的不等式![]() ;
;
(3)如果函數(shù)![]() 的圖象恒在直線
的圖象恒在直線![]() 的上方,證明:
的上方,證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,圓![]() :
:![]() .
.

(Ⅰ)若圓C與x軸相切,求圓C的方程;
(Ⅱ)已知![]() ,圓
,圓![]() 與x軸相交于兩點
與x軸相交于兩點![]() (點
(點![]() 在點
在點![]() 的左側).過點
的左側).過點![]() 任作一條直線與圓
任作一條直線與圓![]() :
:![]() 相交于兩點A,B.問:是否存在實數(shù)a,使得
相交于兩點A,B.問:是否存在實數(shù)a,使得![]() =
=![]() ?若存在,求出實數(shù)a的值,若不存在,請說明理由.
?若存在,求出實數(shù)a的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某城市的公交公司為了方便市民出行,科學規(guī)劃車輛投放,在一個人員密集流動地段增設一個起點站,為了研究車輛發(fā)車間隔時間![]() 與乘客等候人數(shù)
與乘客等候人數(shù)![]() 之間的關系,經(jīng)過調查得到如下數(shù)據(jù):
之間的關系,經(jīng)過調查得到如下數(shù)據(jù):
間隔時間/分 | 10 | 11 | 12 | 13 | 14 | 15 |
等候人數(shù)y/人 | 23 | 25 | 26 | 29 | 28 | 31 |
調查小組先從這![]() 組數(shù)據(jù)中選取
組數(shù)據(jù)中選取![]() 組數(shù)據(jù)求線性回歸方程,再用剩下的
組數(shù)據(jù)求線性回歸方程,再用剩下的![]() 組數(shù)據(jù)進行檢驗.檢驗方法如下:先用求得的線性回歸方程計算間隔時間對應的等候人數(shù)
組數(shù)據(jù)進行檢驗.檢驗方法如下:先用求得的線性回歸方程計算間隔時間對應的等候人數(shù)![]() ,再求
,再求![]() 與實際等候人數(shù)
與實際等候人數(shù)![]() 的差,若差值的絕對值都不超過
的差,若差值的絕對值都不超過![]() ,則稱所求方程是“恰當回歸方程”.
,則稱所求方程是“恰當回歸方程”.
(1)從這![]() 組數(shù)據(jù)中隨機選取2組數(shù)據(jù),求選取的這
組數(shù)據(jù)中隨機選取2組數(shù)據(jù),求選取的這![]() 組數(shù)據(jù)的間隔時間不相鄰的概率;
組數(shù)據(jù)的間隔時間不相鄰的概率;
(2)若選取的是后面![]() 組數(shù)據(jù),求
組數(shù)據(jù),求![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ,并判斷此方程是否是“恰當回歸方程”;
,并判斷此方程是否是“恰當回歸方程”;
附:對于一組數(shù)據(jù)![]() ,
,![]() ,……,
,……,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為:
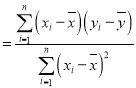 ,
,![]() .
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com