
【題目】以原點(diǎn)為圓心,半徑為![]() 的圓
的圓![]()
![]() 與直線
與直線![]() 相切.
相切.
(1)直線![]() 過(guò)點(diǎn)
過(guò)點(diǎn)![]() 且
且![]() 截圓
截圓![]() 所得弦長(zhǎng)為
所得弦長(zhǎng)為![]() 求直線
求直線![]()
![]() 的方程;
的方程;
(2)設(shè)圓![]() 與
與![]() 軸的正半軸的交點(diǎn)為
軸的正半軸的交點(diǎn)為![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 作兩條斜率分別為
作兩條斜率分別為![]()
![]() 的直線交圓
的直線交圓![]() 于
于![]() 兩點(diǎn),且
兩點(diǎn),且![]()
![]() ,證明:直線
,證明:直線![]() 恒過(guò)一個(gè)定點(diǎn),并求出該定點(diǎn)坐標(biāo).
恒過(guò)一個(gè)定點(diǎn),并求出該定點(diǎn)坐標(biāo).

【答案】(1)![]() 或
或![]()
![]() ;(2)
;(2)![]() .
.
【解析】
分析:(1)先由直線和圓相切得到圓的方程,再由垂徑定理列式,分直線斜率存在與不存在兩種情況得到結(jié)果;(3)聯(lián)立直線和圓,由韋達(dá)定理得到交點(diǎn)的坐標(biāo),由這兩個(gè)點(diǎn)寫(xiě)出直線方程,進(jìn)而得到直線過(guò)定點(diǎn).
詳解:
(1)∵圓![]() 與直線
與直線![]()
![]() 相切,
相切,
∴圓心![]() 到直線的距離為
到直線的距離為![]() ,
,
∴圓![]() 的方程為:
的方程為:![]()
若直線![]() 的斜率不存在,直線
的斜率不存在,直線![]() 為
為![]()
![]() ,
,
此時(shí)直線![]() 截圓所得弦長(zhǎng)為
截圓所得弦長(zhǎng)為![]()
![]() ,符合題意;
,符合題意;
若直線![]() 的斜率存在,設(shè)直線
的斜率存在,設(shè)直線![]() 為
為![]()
![]() ,
,
由題意知,圓心到直線的距離為![]()
![]() ,解得:
,解得:![]() ,
,
此時(shí)直線![]() 為
為![]() ,
,
則所求的直線![]() 為
為![]() 或
或![]()
![]()
(2)由題意知,![]()
![]() ,設(shè)直線
,設(shè)直線![]() ,
,
與圓方程聯(lián)立得:![]()
![]() ,
,
消去![]() 得:
得:![]()
![]() ,
,
∴![]() ∴
∴![]() ,
,![]()
用![]() 換掉
換掉![]() 得到B點(diǎn)坐標(biāo)
得到B點(diǎn)坐標(biāo)
∴![]() ,
,![]()
![]()
∴直線AB的方程為![]()
整理得:![]()
則直線AB恒過(guò)定點(diǎn)為![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知兩條公路![]() 的交匯點(diǎn)
的交匯點(diǎn)![]() 處有一學(xué)校,現(xiàn)擬在兩條公路之間的區(qū)域內(nèi)建一工廠
處有一學(xué)校,現(xiàn)擬在兩條公路之間的區(qū)域內(nèi)建一工廠![]() ,在兩公路旁
,在兩公路旁![]() (異于點(diǎn)
(異于點(diǎn)![]() )處設(shè)兩個(gè)銷(xiāo)售點(diǎn),且滿足
)處設(shè)兩個(gè)銷(xiāo)售點(diǎn),且滿足![]() ,
,![]() (千米),
(千米),![]() (千米),設(shè)
(千米),設(shè)![]() .
.

(1)試用![]() 表示
表示![]() ,并寫(xiě)出
,并寫(xiě)出![]() 的范圍;
的范圍;
(2)當(dāng)![]() 為多大時(shí),工廠產(chǎn)生的噪聲對(duì)學(xué)校的影響最小(即工廠與學(xué)校的距離最遠(yuǎn)).
為多大時(shí),工廠產(chǎn)生的噪聲對(duì)學(xué)校的影響最小(即工廠與學(xué)校的距離最遠(yuǎn)).
(注:![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在某次測(cè)量中得到的A樣本數(shù)據(jù)如下:52,54,54,56,56,56,55,55,55,55.若B樣本數(shù)據(jù)恰好是A樣本數(shù)據(jù)都加6后所得數(shù)據(jù),則A,B兩樣本的下列數(shù)字特征對(duì)應(yīng)相同的是( )
A. 眾數(shù) B. 平均數(shù)
C. 中位數(shù) D. 標(biāo)準(zhǔn)差
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】中國(guó)共產(chǎn)黨第十九次全國(guó)代表大會(huì)于2017年10月24日在北京召開(kāi),會(huì)議提出“決勝全面建成小康社會(huì)”.某市積極響應(yīng)開(kāi)展“脫貧攻堅(jiān)”,為2020年“全面建成小康社會(huì)”貢獻(xiàn)力量.為了解該市農(nóng)村“脫貧攻堅(jiān)“情況,從某縣調(diào)查得到農(nóng)村居民2011年至2017年家庭人均純收入![]() (單位:百元)的數(shù)據(jù)如下表:
(單位:百元)的數(shù)據(jù)如下表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年人均純收入 | 41 | 45 | 48 | 56 | 60 | 64 | 71 |
注:小康的標(biāo)準(zhǔn)是農(nóng)村居民家庭年人均純收入達(dá)到8000元.
(1)求![]() 關(guān)于
關(guān)于![]() 的線性回歸方程;
的線性回歸方程;
(2)利用(1)中的回歸方程,預(yù)測(cè)2020年該縣農(nóng)村居民家庭年人均純收入能否達(dá)到“全面建成小康社會(huì)”的標(biāo)準(zhǔn)?
附:回歸直線![]() 的斜率和截距的最小二乘估計(jì)公式分別為:
的斜率和截距的最小二乘估計(jì)公式分別為:
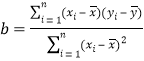 ,
,![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】將邊長(zhǎng)為2的正![]() 沿著高
沿著高![]() 折起,使
折起,使![]() ,若折起后
,若折起后![]() 四點(diǎn)都在球
四點(diǎn)都在球![]() 的表面上,則球
的表面上,則球![]() 的表面積為( )
的表面積為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù) ![]() 的定義域?yàn)镽.
的定義域?yàn)镽.
(1)求實(shí)數(shù)m的范圍;
(2)若m的最大值為n,當(dāng)正數(shù)a,b滿足 ![]() 時(shí),求4a+7b的最小值.
時(shí),求4a+7b的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓C: ![]() (a>b>0)的一個(gè)頂點(diǎn)為A(2,0),離心率為
(a>b>0)的一個(gè)頂點(diǎn)為A(2,0),離心率為![]() .直線y=k(x-1)與橢圓C交于不同的兩點(diǎn)M,N.
.直線y=k(x-1)與橢圓C交于不同的兩點(diǎn)M,N.
(1)求橢圓C的方程;
(2)當(dāng)△AMN的面積為![]() 時(shí),求k的值.
時(shí),求k的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某公司計(jì)劃購(gòu)買(mǎi)1臺(tái)機(jī)器,該種機(jī)器使用三年后即被淘汰.機(jī)器有一易損零件,在購(gòu)進(jìn)機(jī)器時(shí),可以額外購(gòu)買(mǎi)這種零件作為備件,每個(gè)200元.在機(jī)器使用期間,如果備件不足再購(gòu)買(mǎi),則每個(gè)500元.現(xiàn)需決策在購(gòu)買(mǎi)機(jī)器時(shí)應(yīng)同時(shí)購(gòu)買(mǎi)幾個(gè)易損零件,為此搜集并整理了100臺(tái)這種機(jī)器在三年使用期內(nèi)更換的易損零件數(shù),得下面柱狀圖.

記![]() 表示
表示![]() 臺(tái)機(jī)器在三年使用期內(nèi)需更換的易損零件數(shù),
臺(tái)機(jī)器在三年使用期內(nèi)需更換的易損零件數(shù),![]() 表示
表示![]() 臺(tái)機(jī)器在購(gòu)買(mǎi)易損零件上所需的費(fèi)用(單位:元),
臺(tái)機(jī)器在購(gòu)買(mǎi)易損零件上所需的費(fèi)用(單位:元),![]() 表示購(gòu)機(jī)的同時(shí)購(gòu)買(mǎi)的易損零件數(shù).
表示購(gòu)機(jī)的同時(shí)購(gòu)買(mǎi)的易損零件數(shù).
(1)若![]() ,求
,求![]() 與
與![]() 的函數(shù)解析式;
的函數(shù)解析式;
(2)若要求 “需更換的易損零件數(shù)不大于![]() ”的頻率不小于
”的頻率不小于![]() ,求
,求![]() 的最小值;
的最小值;
(3)假設(shè)這![]() 臺(tái)機(jī)器在購(gòu)機(jī)的同時(shí)每臺(tái)都購(gòu)買(mǎi)
臺(tái)機(jī)器在購(gòu)機(jī)的同時(shí)每臺(tái)都購(gòu)買(mǎi)![]() 個(gè)易損零件,或每臺(tái)都購(gòu)買(mǎi)
個(gè)易損零件,或每臺(tái)都購(gòu)買(mǎi)![]() 個(gè)易損零件,分別計(jì)算這
個(gè)易損零件,分別計(jì)算這![]() 臺(tái)機(jī)器在購(gòu)買(mǎi)易損零件上所需費(fèi)用的平均數(shù),以此作為決策依據(jù),購(gòu)買(mǎi)
臺(tái)機(jī)器在購(gòu)買(mǎi)易損零件上所需費(fèi)用的平均數(shù),以此作為決策依據(jù),購(gòu)買(mǎi)![]() 臺(tái)機(jī)器的同時(shí)應(yīng)購(gòu)買(mǎi)
臺(tái)機(jī)器的同時(shí)應(yīng)購(gòu)買(mǎi)![]() 個(gè)還是
個(gè)還是![]() 個(gè)易損零件?
個(gè)易損零件?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】經(jīng)銷(xiāo)商小王對(duì)其所經(jīng)營(yíng)的某一型號(hào)二手汽車(chē)的使用年數(shù)![]() (0<
(0<![]() ≤10)與銷(xiāo)售價(jià)格
≤10)與銷(xiāo)售價(jià)格![]() (單位:萬(wàn)元/輛)進(jìn)行整理,得到如下的對(duì)應(yīng)數(shù)據(jù):
(單位:萬(wàn)元/輛)進(jìn)行整理,得到如下的對(duì)應(yīng)數(shù)據(jù):
使用年數(shù) | 2 | 4 | 6 | 8 | 10 |
售價(jià) | 16 | 13 | 9.5 | 7 | 4.5 |
(Ⅰ)試求![]() 關(guān)于
關(guān)于![]() 的回歸直線方程;
的回歸直線方程;
(附:回歸方程![]() 中,
中,
(Ⅱ)已知每輛該型號(hào)汽車(chē)的收購(gòu)價(jià)格為![]() 萬(wàn)元,根據(jù)(Ⅰ)中所求的回歸方程,
萬(wàn)元,根據(jù)(Ⅰ)中所求的回歸方程,
預(yù)測(cè)![]() 為何值時(shí),小王銷(xiāo)售一輛該型號(hào)汽車(chē)所獲得的利潤(rùn)
為何值時(shí),小王銷(xiāo)售一輛該型號(hào)汽車(chē)所獲得的利潤(rùn)![]() 最大.
最大.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com