
(1)求函數g(x)的解析式;
(2)解不等式g(x)≥f(x)-|x-1|;
(3)若h(x)=g(x)-λf(x)+1在[-1,1]上是增函數,求實數λ的取值范圍.
解析:此題考查綜合應用函數的奇偶性和增減性解決解析式和最值問題.
解:(1)設函數y=f(x)的圖象上任一點Q(x0,y0)關于原點的對稱點為P(x,y),?
則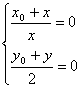 即
即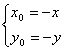
∵點Q(x0,y0)在函數y=f(x)的圖象上,?
∴-y=x2-2x,即y=-x2+2x.?
故g(x)=-x2+2x.?
(2)由g(x)≥f(x)-|x-1|,可得2x2-|x-1|≤0.?
當x≥1時,2x2-x+1≤0.?
此時不等式無解.?
當x<1時,2x2-x+1≤0.?
∴-1≤x≤![]() .?
.?
因此,原不等式的解集為[-1, ![]() ].?
].?
(3)h(x)=-(1+λ)x2+2(1-λ)x+1.?
①當λ=-1時,h(x)=4x+1在[-1,1]上是增函數,∴λ=-1.?
②當λ≠-1時,對稱軸的方程為x=![]() .
.
(ⅰ)當λ<-1時,![]() ≤-1,解得λ<-1.
≤-1,解得λ<-1.
(ⅱ)當λ>-1時,![]() ≥1時,解得-1<λ≤0.?
≥1時,解得-1<λ≤0.?
綜上,λ≤0.


科目:高中數學 來源: 題型:
(1)求函數g(x)的解析式;
(2)解不等式g(x)≥f(x)-|x-1|;
(3)(文)若h(x)=g(x)-λf(x)+1在[-1,1]上是增函數,求實數λ的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
已知函數f(x)和g(x)分別由下表給出定義:
| x | 1 | 2 | 3 |
| f(x) | 2 | ________ | 3 |
| x | 1 | 2 | 3 |
| g(x) | 3 | ________ | 1 |
若方程f(g(x))=g(f(x))的解恰有2個,請在表中橫線上填上合適的數.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年江西省高三上學期期中考試文科數學試卷(解析版) 題型:解答題
已知函數f(x)和g(x)的圖象關于原點對稱,且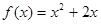
(1)求函數g(x)的解析式;
(2)解不等式 ;
;
(3)若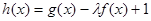 在[-1,1]上是增函數,求實數
在[-1,1]上是增函數,求實數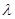 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源:新課標高三數學函數的圖象奇偶性、周期性專項訓練(河北) 題型:解答題
已知函數f(x)和g(x)的圖象關于原點對稱,且f(x)=x2+2x.
(1)求函數g(x)的解析式;
(2)解不等式g(x)≥f(x)-|x-1|;
(3)若h(x)=g(x)-λf(x)+1在[-1,1]上是增函數,求實數λ的取值范圍
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com