
���}Ŀ����֪�E�A![]() �İ뽹����
�İ뽹����![]() ���A
���A![]() �c�E�A
�c�E�A![]() ���҃H�Ѓɂ�(g��)�����c(di��n)��ֱ��
���҃H�Ѓɂ�(g��)�����c(di��n)��ֱ��![]() �c�E�A
�c�E�A![]() ֻ��һ��(g��)�����c(di��n).
ֻ��һ��(g��)�����c(di��n).
��1����E�A![]() �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2����֪?ji��ng)�ֱ��![]() �^�E�A
�^�E�A![]() �����c(di��n)
�����c(di��n)![]() �����c�E�A
�����c�E�A![]() �քe����
�քe����![]() ���c(di��n)��ԇ����
���c(di��n)��ԇ����![]() �S���Ƿ���ڶ��c(di��n)
�S���Ƿ���ڶ��c(di��n)![]() ��ʹ��
��ʹ��![]() �鶨ֵ?�����ڣ����ԓ��ֵ���c(di��n)
�鶨ֵ?�����ڣ����ԓ��ֵ���c(di��n)![]() ������(bi��o)���������ڣ�Ո�f������.
������(bi��o)���������ڣ�Ո�f������.
���𰸡���1��![]() ��2����
��2����![]() �S�ϴ����c(di��n)
�S�ϴ����c(di��n)![]() ��ʹ��
��ʹ��![]() �鶨ֵ
�鶨ֵ![]()
��������
��1������(j��)��֪���![]() ���ÙE�A
���ÙE�A![]() �Ę�(bi��o)��(zh��n)���̣���2����(d��ng)ֱ��
�Ę�(bi��o)��(zh��n)���̣���2����(d��ng)ֱ��![]() ��б�ʴ��ڕr(sh��)���O(sh��)ֱ��
��б�ʴ��ڕr(sh��)���O(sh��)ֱ��![]() �ķ��̞�
�ķ��̞�![]() ���O(sh��)
���O(sh��)![]() �������f�_(d��)�����������Ĕ�(sh��)���e���
�������f�_(d��)�����������Ĕ�(sh��)���e���![]() ���˕r(sh��)
���˕r(sh��)![]() �鶨ֵ
�鶨ֵ![]() ����(d��ng)ֱ��
����(d��ng)ֱ��![]() ��б�ʲ����ڕr(sh��)��ֱ��
��б�ʲ����ڕr(sh��)��ֱ��![]() �ķ��̞�
�ķ��̞�![]() ������˕r(sh��)�c(di��n)RҲ�M��ǰ��ĽY(ji��)Փ�����ý�.
������˕r(sh��)�c(di��n)RҲ�M��ǰ��ĽY(ji��)Փ�����ý�.
(1)���}�⣬��![]() ��
��
�t![]() ��
��
�ʙE�A�Ę�(bi��o)��(zh��n)���̞�![]() .
.
![]() ��(d��ng)ֱ��
��(d��ng)ֱ��![]() ��б�ʴ��ڕr(sh��)���O(sh��)ֱ��
��б�ʴ��ڕr(sh��)���O(sh��)ֱ��![]() �ķ��̞�
�ķ��̞�![]() ��
��
���˙E�A![]() �ķ��̣��ɵ�
�ķ��̣��ɵ�![]()
�O(sh��)![]() ��
��![]() ���t
���t![]() ��
��![]()
�O(sh��)![]() ���t
���t![]()
![]()
![]()
![]()
![]()
��![]() �鶨ֵ���t
�鶨ֵ���t![]() �����
�����![]()
�˕r(sh��)![]()
![]() �c(di��n)������(bi��o)��
�c(di��n)������(bi��o)��![]()
�ڮ�(d��ng)ֱ��![]() ��б�ʲ����ڕr(sh��)��ֱ��
��б�ʲ����ڕr(sh��)��ֱ��![]() �ķ��̞�
�ķ��̞�![]() ������
������![]() ����
����
�����O(sh��)![]() ����
����![]() ���t
���t![]()
![]()
�C����������![]() �S�ϴ����c(di��n)
�S�ϴ����c(di��n)![]() ��ʹ��
��ʹ��![]() �鶨ֵ
�鶨ֵ![]()



| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
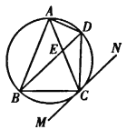
���}Ŀ����D��![]() ��(n��i)����
��(n��i)����![]() ��
��![]() ��ֱ��
��ֱ��![]() ��
��![]() ���c(di��n)
���c(di��n)![]() ����
����![]() ��
��![]() �c
�c![]() �����c(di��n)
�����c(di��n)![]() .
.
(1)���C��![]() ��
��
(2)��![]() ��
��![]() ����
����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]()
![]() .
.
��������(d��ng)![]() �r(sh��)����(sh��)
�r(sh��)����(sh��)![]() ��
��![]() ̎���о����̣�
̎���о����̣�
��������(d��ng)![]() �r(sh��)����(sh��)
�r(sh��)����(sh��)![]() ���{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
������������(sh��)![]() �Ѓɂ�(g��)�Oֵ�c(di��n)
�Ѓɂ�(g��)�Oֵ�c(di��n)![]() ������ʽ
������ʽ![]() ���������(sh��)��(sh��)
���������(sh��)��(sh��)![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪ż����(sh��)![]() �M��
�M��![]() ��
��![]() ����(d��ng)
����(d��ng)![]() �r(sh��),
�r(sh��),![]() ���P(gu��n)��
���P(gu��n)��![]() �IJ���ʽ
�IJ���ʽ![]() ��
��![]() ������ֻ��200��(g��)����(sh��)�⣬�t��(sh��)��(sh��)
������ֻ��200��(g��)����(sh��)�⣬�t��(sh��)��(sh��)![]() ��ȡֵ�����飨 ��
��ȡֵ�����飨 ��
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��
��1����ô����![]() �څ^(q��)�g
�څ^(q��)�g![]() �ϵĸ��Ă�(g��)��(sh��)��___________��
�ϵĸ��Ă�(g��)��(sh��)��___________��
��2�������������}��
�ٺ���(sh��)![]() �����ں���(sh��)��
�����ں���(sh��)��
�ں���(sh��)![]() �������ֵ������Сֵ��
�������ֵ������Сֵ��
�ۺ���(sh��)![]() �Ķ��x����
�Ķ��x����![]() ������D���Ќ��Q�S��
������D���Ќ��Q�S��
�����_�^(q��)�g![]() �ϣ�
�ϣ�![]() ���{(di��o)�f�p��
���{(di��o)�f�p��
���������}����̖��______________��������}����̖����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D����֪����ֱ��������![]() ��б߅
��б߅![]() ����ֱ�����̞�
����ֱ�����̞�![]() ������
������![]() �c(di��n)��
�c(di��n)��![]() �c(di��n)�Ϸ���ֱ����c(di��n)
�c(di��n)�Ϸ���ֱ����c(di��n)![]() ������(bi��o)��
������(bi��o)��![]() ��
��

��1����![]() ߅�ϵĸ߾�
߅�ϵĸ߾�![]() ����ֱ���ķ��̣�
����ֱ���ķ��̣�
��2�������ֱ��������![]() ����ӈA�Ę�(bi��o)��(zh��n)���̣�
����ӈA�Ę�(bi��o)��(zh��n)���̣�
��3���քe���ֱ��߅![]() ��
��![]() ����ֱ���ķ��̣�
����ֱ���ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��һֻ�t��x�Įa(ch��n)�є�(sh��)![]() �͜ض�
�͜ض�![]() ���P(gu��n)���F(xi��n)�ռ���4�M�^�y��(sh��)��(j��)�����±��У�����(j��)��(sh��)��(j��)����ɢ�c(di��n)�D���£�
���P(gu��n)���F(xi��n)�ռ���4�M�^�y��(sh��)��(j��)�����±��У�����(j��)��(sh��)��(j��)����ɢ�c(di��n)�D���£�
�ض� | 20 | 25 | 30 | 35 |
�a(ch��n)�є�(sh��) | 5 | 20 | 100 | 325 |

������(sh��)��(j��):![]() ��
��![]() ��
��![]() ,
,
![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,
![]() ,
,![]()
| 5 | 20 | 100 | 325 |
| 1.61 | 3 | 4.61 | 5.78 |
��1������(j��)ɢ�c(di��n)�D�Д�![]() �c
�c![]() ��һ��(g��)���m������a(ch��n)�є�(sh��)
��һ��(g��)���m������a(ch��n)�є�(sh��)![]() �P(gu��n)�ڜض�
�P(gu��n)�ڜض�![]() �Ļؚw������ͣ����o���Д༴�ɣ������f�����ɣ�
�Ļؚw������ͣ����o���Д༴�ɣ������f�����ɣ�
��2������(j��)��1������Y(ji��)��������(sh��)��(j��)������![]() �P(gu��n)��
�P(gu��n)��![]() �Ļؚw���̣���(sh��)�ֱ���2λС��(sh��)����
�Ļؚw���̣���(sh��)�ֱ���2λС��(sh��)����
��3��Ҫʹ�îa(ch��n)�є�(sh��)�����^50���t�ضȿ����ڶ���![]() ���£������Y(ji��)������������(sh��)��
���£������Y(ji��)������������(sh��)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��
����(d��ng)![]() �r(sh��)��������
�r(sh��)��������![]() ���c(di��n)
���c(di��n)![]() ̎���о����̣�
̎���о����̣�
����(d��ng)![]() �r(sh��)�����C��
�r(sh��)�����C��![]() ������
������![]() ����.
����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���W(xu��)У�Έ@������@��һ��(g��)�Α��(xi��ng)Ŀ:���������b��3��(g��)����2��(g��)����,���������b��1��(g��)����2��(g��)����,�@Щ����ɫ����ȫ��ͬ.ÿ���Α���@�ɂ�(g��)��������S�C(j��)����2��(g��)��,�������İ�������2��(g��),�t�@��(ji��ng).(ÿ���Α�Y(ji��)������Ż�ԭ��)
��1������1���Α���,
������3��(g��)����ĸ���;
�ګ@��(ji��ng)�ĸ���;
��2������2���Α��Ы@��(ji��ng)�Δ�(sh��)![]() �ķֲ���.
�ķֲ���.
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com