
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
在平面直角坐標(biāo)系中,已知點(diǎn)![]() ,曲線
,曲線![]() 的參數(shù)方程為
的參數(shù)方程為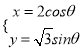 (
(![]() 為參數(shù)),以坐標(biāo)原點(diǎn)
為參數(shù)),以坐標(biāo)原點(diǎn)![]() 為極點(diǎn),以
為極點(diǎn),以![]() 軸正半軸為極軸,建立極坐標(biāo)系,點(diǎn)
軸正半軸為極軸,建立極坐標(biāo)系,點(diǎn)![]() 的極坐標(biāo)為
的極坐標(biāo)為![]() ,直線
,直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,且
,且![]() 過(guò)點(diǎn)
過(guò)點(diǎn)![]() ;過(guò)點(diǎn)
;過(guò)點(diǎn)![]() 與直線
與直線![]() 平行的直線為
平行的直線為![]() ,
, ![]() 與曲線
與曲線![]() 相交于兩點(diǎn)
相交于兩點(diǎn)![]() .
.
(1)求曲線![]() 上的點(diǎn)到直線
上的點(diǎn)到直線![]() 距離的最小值;
距離的最小值;
(2)求![]() 的值.
的值.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】試題分析:(1)將![]() 點(diǎn)坐標(biāo)代入直線的極坐標(biāo)方程,求得
點(diǎn)坐標(biāo)代入直線的極坐標(biāo)方程,求得![]() 的值,展開(kāi)后可將直線的極坐標(biāo)方程轉(zhuǎn)化為直角坐標(biāo)方程.利用點(diǎn)到直線的距離公式求出
的值,展開(kāi)后可將直線的極坐標(biāo)方程轉(zhuǎn)化為直角坐標(biāo)方程.利用點(diǎn)到直線的距離公式求出![]() 的表達(dá)式,利用三角函數(shù)輔助角公式可求得距離的最小值.(2)利用點(diǎn)
的表達(dá)式,利用三角函數(shù)輔助角公式可求得距離的最小值.(2)利用點(diǎn)![]() 的坐標(biāo)和斜率可求得
的坐標(biāo)和斜率可求得![]() 的方程,寫出
的方程,寫出![]() 的參數(shù)方程,代入曲線
的參數(shù)方程,代入曲線![]() 的普通方程,化簡(jiǎn)后寫出韋達(dá)定理,利用弦長(zhǎng)公式可求得
的普通方程,化簡(jiǎn)后寫出韋達(dá)定理,利用弦長(zhǎng)公式可求得![]() 的值.
的值.
試題解析:
(1)因?yàn)?/span>![]() ,且
,且![]() ,所以
,所以![]() ,即
,即![]()
所以直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]()
所以![]()
即直線![]() 的直角坐標(biāo)方程為
的直角坐標(biāo)方程為![]()
設(shè)曲線![]() 上的點(diǎn)到直線
上的點(diǎn)到直線![]() 距離為
距離為![]() ,則
,則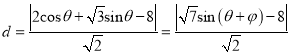
所以曲線![]() 上的點(diǎn)到直線
上的點(diǎn)到直線![]() 距離的最小值為
距離的最小值為
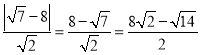
(2)設(shè)![]() 的方程為
的方程為![]() ,由于
,由于![]() 過(guò)點(diǎn)
過(guò)點(diǎn)![]() ,所以
,所以![]() ,所以
,所以![]() 的方程為
的方程為![]()
故![]() 的參數(shù)方程為
的參數(shù)方程為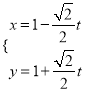 (
(![]() 為參數(shù)),曲線
為參數(shù)),曲線![]() 的普通方程為
的普通方程為![]()
所以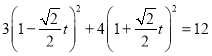 ,即有
,即有![]()
所以![]()
所以![]()
![]()


 A加金題 系列答案
A加金題 系列答案 全優(yōu)測(cè)試卷系列答案
全優(yōu)測(cè)試卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】(本小題12分)已知平行四邊形![]() 的三個(gè)頂點(diǎn)的坐標(biāo)為
的三個(gè)頂點(diǎn)的坐標(biāo)為![]() ,
,![]() ,
,![]() .
.
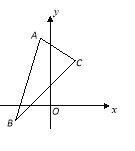
(Ⅰ)在![]() ABC中,求邊AC中線所在直線方程;
ABC中,求邊AC中線所在直線方程;
(Ⅱ)求平行四邊形![]() 的頂點(diǎn)D的坐標(biāo)及邊BC的長(zhǎng)度;
的頂點(diǎn)D的坐標(biāo)及邊BC的長(zhǎng)度;
(Ⅲ)求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)△ABC的內(nèi)角A,B,C對(duì)邊分別為a,b,c,已知A=60°,a= ![]() ,sinB+sinC=6
,sinB+sinC=6 ![]() sinBsinC,則△ABC的面積為 .
sinBsinC,則△ABC的面積為 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知正項(xiàng)數(shù)列{an}的前n項(xiàng)和為Sn , 數(shù)列{an}滿足,2Sn=an(an+1).
(1)求數(shù)列{an}的通項(xiàng)公式;
(2)設(shè)數(shù)列{ ![]() }的前n項(xiàng)和為An , 求證:對(duì)任意正整數(shù)n,都有An<
}的前n項(xiàng)和為An , 求證:對(duì)任意正整數(shù)n,都有An< ![]() 成立;
成立;
(3)數(shù)列{bn}滿足bn=( ![]() )nan , 它的前n項(xiàng)和為Tn , 若存在正整數(shù)n,使得不等式(﹣2)n﹣1λ<Tn+
)nan , 它的前n項(xiàng)和為Tn , 若存在正整數(shù)n,使得不等式(﹣2)n﹣1λ<Tn+ ![]() ﹣2n﹣1成立,求實(shí)數(shù)λ的取值范圍.
﹣2n﹣1成立,求實(shí)數(shù)λ的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]()
![]() 經(jīng)過(guò)點(diǎn)
經(jīng)過(guò)點(diǎn)![]() ,一個(gè)焦點(diǎn)是
,一個(gè)焦點(diǎn)是![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若傾斜角為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點(diǎn),且
兩點(diǎn),且![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() 的中心在坐標(biāo)原點(diǎn),焦點(diǎn)在
的中心在坐標(biāo)原點(diǎn),焦點(diǎn)在![]() 軸上,左頂點(diǎn)為
軸上,左頂點(diǎn)為![]() ,左焦點(diǎn)為
,左焦點(diǎn)為![]() ,點(diǎn)
,點(diǎn)![]() 在橢圓
在橢圓![]() 上,直線
上,直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
, ![]() 兩點(diǎn),直線
兩點(diǎn),直線![]() ,
, ![]() 分別與
分別與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,
, ![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)以![]() 為直徑的圓是否經(jīng)過(guò)定點(diǎn)?若經(jīng)過(guò),求出定點(diǎn)的坐標(biāo);若不經(jīng)過(guò),請(qǐng)說(shuō)明理由.
為直徑的圓是否經(jīng)過(guò)定點(diǎn)?若經(jīng)過(guò),求出定點(diǎn)的坐標(biāo);若不經(jīng)過(guò),請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,多面體![]() 中,四邊形
中,四邊形![]() 是菱形,
是菱形, ![]() ,
, ![]() 相交于
相交于![]() ,
, ![]() ,點(diǎn)
,點(diǎn)![]() 在平面
在平面![]() 上的射影恰好是線段
上的射影恰好是線段![]() 的中點(diǎn).
的中點(diǎn).

(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)若直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,求平面
,求平面![]() 與平面
與平面![]() 所成角(銳角)的余弦值.
所成角(銳角)的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知向量 ![]() =(1,2),
=(1,2), ![]() =(cosα,sinα),設(shè)
=(cosα,sinα),設(shè) ![]() =
= ![]() ﹣t
﹣t ![]() (t為實(shí)數(shù)).
(t為實(shí)數(shù)).
(1)t=1 時(shí),若 ![]() ∥
∥ ![]() ,求2cos2α﹣sin2α的值;
,求2cos2α﹣sin2α的值;
(2)若α= ![]() ,求|
,求| ![]() |的最小值,并求出此時(shí)向量
|的最小值,并求出此時(shí)向量 ![]() 在
在 ![]() 方向上的投影.
方向上的投影.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知向量 ![]() =(sin
=(sin ![]() ,sin
,sin ![]() ),
), ![]() =(cos
=(cos ![]() ,cos
,cos ![]() ),且向量
),且向量 ![]() 與向量
與向量 ![]() 共線.
共線.
(1)求證:sin( ![]() ﹣
﹣ ![]() )=0;
)=0;
(2)若記函數(shù)f(x)=sin( ![]() ﹣
﹣ ![]() ),求函數(shù)f(x)的對(duì)稱軸方程;
),求函數(shù)f(x)的對(duì)稱軸方程;
(3)求f(1)+f(2)+f(3)+…+f(2013)的值;
(4)如果已知角0<A<B<π,且A+B+C=π,滿足f( ![]() )=f(
)=f( ![]() )=
)= ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com