
【題目】如圖1,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,點E在
,點E在![]() 上,且
上,且![]() ,將三角形
,將三角形![]() 沿線段
沿線段![]() 折起到
折起到![]() 的位置,
的位置,![]() (如圖2).
(如圖2).
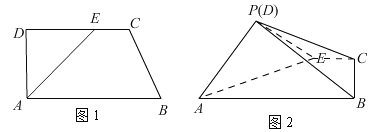
(1)求證:平面![]() 平面
平面![]() ;
;
(2)在線段![]() 上是否存在點M,使
上是否存在點M,使![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的普通方程為
的普通方程為![]() ,以原點
,以原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標(biāo)系,曲線
軸正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(I)求![]() 的參數(shù)方程與
的參數(shù)方程與![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(II)射線![]() 與
與![]() 交于異于極點的點
交于異于極點的點![]() ,與
,與![]() 的交點為
的交點為![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]() .
.
(1)若![]() 為等差數(shù)列,且
為等差數(shù)列,且![]()
①求該等差數(shù)列的公差![]() ;
;
②設(shè)數(shù)列![]() 滿足
滿足![]() ,則當(dāng)
,則當(dāng)![]() 為何值時,
為何值時,![]() 最大?請說明理由;
最大?請說明理由;
(2)若![]() 還同時滿足:
還同時滿足:
①![]() 為等比數(shù)列;
為等比數(shù)列;
②![]() ;
;
③對任意的正整數(shù)![]() 存在自然數(shù)
存在自然數(shù)![]() ,使得
,使得![]() 、
、![]() 、
、![]() 依次成等差數(shù)列,試求數(shù)列
依次成等差數(shù)列,試求數(shù)列![]() 的通項公式.
的通項公式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2019年春節(jié)期間,我國高速公路繼續(xù)執(zhí)行“節(jié)假日高速公路免費政策”某路橋公司為掌握春節(jié)期間車輛出行的高峰情況,在某高速公路收費點記錄了大年初三上午9:20~10:40這一時間段內(nèi)通過的車輛數(shù),統(tǒng)計發(fā)現(xiàn)這一時間段內(nèi)共有600輛車通過該收費點,它們通過該收費點的時刻的頻率分布直方圖如下圖所示,其中時間段9:20~9:40記作區(qū)間![]() ,9:40~10:00記作
,9:40~10:00記作![]() ,10:00~10:20記作
,10:00~10:20記作![]() ,10:20~10:40記作
,10:20~10:40記作![]() .例如:10點04分,記作時刻64.
.例如:10點04分,記作時刻64.
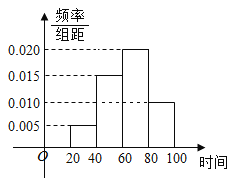
(1)估計這600輛車在9:20~10:40時間段內(nèi)通過該收費點的時刻的平均值(同一組中的數(shù)據(jù)用該組區(qū)間的中點值代表);
(2)為了對數(shù)據(jù)進行分析,現(xiàn)采用分層抽樣的方法從這600輛車中抽取10輛,再從這10輛車中隨機抽取4輛,設(shè)抽到的4輛車中,在9:20~10:00之間通過的車輛數(shù)為X,求X的分布列與數(shù)學(xué)期望;
(3)由大數(shù)據(jù)分析可知,車輛在每天通過該收費點的時刻T服從正態(tài)分布![]() ,其中
,其中![]() 可用這600輛車在9:20~10:40之間通過該收費點的時刻的平均值近似代替,
可用這600輛車在9:20~10:40之間通過該收費點的時刻的平均值近似代替,![]() 可用樣本的方差近似代替(同一組中的數(shù)據(jù)用該組區(qū)間的中點值代表),已知大年初五全天共有1000輛車通過該收費點,估計在9:46~10:40之間通過的車輛數(shù)(結(jié)果保留到整數(shù)).
可用樣本的方差近似代替(同一組中的數(shù)據(jù)用該組區(qū)間的中點值代表),已知大年初五全天共有1000輛車通過該收費點,估計在9:46~10:40之間通過的車輛數(shù)(結(jié)果保留到整數(shù)).
參考數(shù)據(jù):若![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的長軸長為
的長軸長為![]() ,且離心率為
,且離心率為![]() .
.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)設(shè)橢圓![]() 的左焦點為
的左焦點為![]() ,點
,點![]() 是橢圓與
是橢圓與![]() 軸負(fù)半軸的交點,經(jīng)過
軸負(fù)半軸的交點,經(jīng)過![]() 的直線
的直線![]() 與橢圓交于點
與橢圓交于點![]() ,經(jīng)過
,經(jīng)過![]() 且與
且與![]() 平行的直線與橢圓交于點
平行的直線與橢圓交于點![]() ,若
,若![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】隨著經(jīng)濟模式的改變,微商和電商已成為當(dāng)今城鄉(xiāng)一種新型的購銷平臺.已知經(jīng)銷某種商品的電商在任何一個銷售季度內(nèi),每售出![]() 噸該商品可獲利潤
噸該商品可獲利潤![]() 萬元,未售出的商品,每
萬元,未售出的商品,每![]() 噸虧損
噸虧損![]() 萬元.根據(jù)往年的銷售經(jīng)驗,得到一個銷售季度內(nèi)市場需求量的頻率分布直方圖如圖所示.已知電商為下一個銷售季度籌備了
萬元.根據(jù)往年的銷售經(jīng)驗,得到一個銷售季度內(nèi)市場需求量的頻率分布直方圖如圖所示.已知電商為下一個銷售季度籌備了![]() 噸該商品.現(xiàn)以
噸該商品.現(xiàn)以![]() (單位:噸,
(單位:噸,![]() )表示下一個銷售季度的市場需求量,
)表示下一個銷售季度的市場需求量,![]() (單位:萬元)表示該電商下一個銷售季度內(nèi)經(jīng)銷該商品獲得的利潤.
(單位:萬元)表示該電商下一個銷售季度內(nèi)經(jīng)銷該商品獲得的利潤.
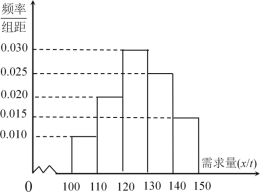
(1)將![]() 表示為
表示為![]() 的函數(shù),求出該函數(shù)表達式;
的函數(shù),求出該函數(shù)表達式;
(2)根據(jù)直方圖估計利潤![]() 不少于57萬元的概率;
不少于57萬元的概率;
(3)根據(jù)頻率分布直方圖,估計一個銷售季度內(nèi)市場需求量![]() 的平均數(shù)與中位數(shù)的大小(保留到小數(shù)點后一位).
的平均數(shù)與中位數(shù)的大小(保留到小數(shù)點后一位).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)![]() 中,圓
中,圓![]() ,圓
,圓![]() 。
。
(Ⅰ)在以O為極點,x軸正半軸為極軸的極坐標(biāo)系中,分別寫出圓![]() 的極坐標(biāo)方程,并求出圓
的極坐標(biāo)方程,并求出圓![]() 的交點坐標(biāo)(用極坐標(biāo)表示);
的交點坐標(biāo)(用極坐標(biāo)表示);
(Ⅱ)求圓![]() 的公共弦的參數(shù)方程。
的公共弦的參數(shù)方程。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在極坐標(biāo)系中,已知曲線C1:ρ=2cosθ和曲線C2:ρcosθ=3,以極點O為坐標(biāo)原點,極軸為x軸非負(fù)半軸建立平面直角坐標(biāo)系.
(1)求曲線C1和曲線C2的直角坐標(biāo)方程;
(2)若點P是曲線C1上一動點,過點P作線段OP的垂線交曲線C2于點Q,求線段PQ長度的最小值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com