
���}Ŀ��������![]() �У�
��![]() ��
��![]() ��
��![]() �����c(di��n)������
�����c(di��n)������![]() �c
�c![]() ����
����![]() �c(di��n)����D1��.��
�c(di��n)����D1��.��![]() ��
��![]() ����
����![]() ��λ�ã�ʹ�ö����
��λ�ã�ʹ�ö����![]() ��ֱ����ǣ���D2��.
��ֱ����ǣ���D2��.
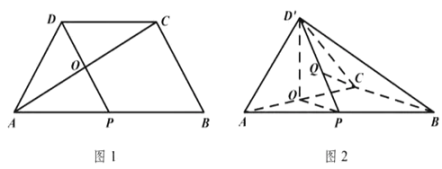
��1�����C��![]() ƽ��
ƽ��![]() ��
��
��2������![]() ���Ƿ�����c(di��n)
���Ƿ�����c(di��n)![]() ��ʹ��
��ʹ��![]() �cƽ��
�cƽ��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��![]() �������ڣ����
�������ڣ����![]() ��ֵ���������ڣ�Ո�f������.
��ֵ���������ڣ�Ո�f������.
���𰸡���1���C��Ҋ������2������![]() �ϴ����c(di��n)
�ϴ����c(di��n)![]() ����
����![]()
��������
��1���ƌ�(d��o)��![]() ���Ķ���߅��
���Ķ���߅��![]() ��ƽ����߅�Σ��ƌ�(d��o)��
��ƽ����߅�Σ��ƌ�(d��o)��![]() ���ɴ����C��
���ɴ����C��![]() ƽ��
ƽ��![]() ��
��
��2���������gֱ������(bi��o)ϵ![]() ���O(sh��)
���O(sh��)![]() ���������������������
���������������������![]() �ϴ����c(di��n)
�ϴ����c(di��n)![]() ����
����![]() �r(sh��)��ʹ��CQ�cƽ��BCD�����ɽǵ�����ֵ��
�r(sh��)��ʹ��CQ�cƽ��BCD�����ɽǵ�����ֵ��![]() .
.
��1���C������?y��n)������?/span>![]() ��
��![]() ��
��![]() ��
��![]() �����c(di��n)��
�����c(di��n)��
����![]() ��
��
������߅��![]() ��ƽ����߅�Σ�
��ƽ����߅�Σ�
��?y��n)龀��![]() �c
�c![]() ����
����![]() �c(di��n)��
�c(di��n)��
����![]() �龀��
�龀��![]() �����c(di��n)��
�����c(di��n)��
����![]() ��
��![]() ��
��
��?y��n)?/span>![]() ƽ��
ƽ��![]() ��
��![]() ƽ��
ƽ��![]() ��
��
����![]() ƽ��
ƽ��![]() .
.
��2���⣺ƽ����߅��![]() �У�
��![]() ��
��
������߅��![]() �����Σ�
������![]() �������
�������![]() ��
��
����![]() ��
��
��?y��n)?/span>![]() ƽ��
ƽ��![]() ��
��![]() ƽ��
ƽ��![]() ��
��
����![]() �Ƕ����
�Ƕ����![]() ��ƽ��ǣ�
��ƽ��ǣ�
��?y��n)����?/span>![]() ��ֱ����ǣ�
��ֱ����ǣ�
����![]() ����
����![]() .
.
������D�������gֱ������(bi��o)ϵ![]() ������
������![]() ��
��
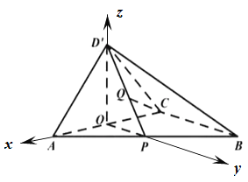
��?y��n)��ڈD1����![]() �У�
��![]() ��
��
����![]() ��
��
����![]() ��
��
����![]() ��
��![]() ��
��
�O(sh��)![]() ��ƽ��
��ƽ��![]() �ķ�������
�ķ�������
��?y��n)?/span> ������
������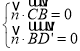 ����
����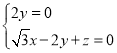 ��
��
ȡ![]() ���õ�
���õ�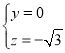 ��
��
����![]() ��
��
����![]() �ϴ����c(di��n)
�ϴ����c(di��n)![]() ʹ��
ʹ��![]() �cƽ��
�cƽ��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��![]() ��
��
�O(sh��)![]() ��
��
��?y��n)?/span>![]() ��
��
����![]() ��
��
��?y��n)?/span>![]() ��
��
����![]() ��
��
��?y��n)?/span>![]() ������
������![]() ��
��
���Ծ���![]() �ϴ����c(di��n)
�ϴ����c(di��n)![]() ����
����![]() ��ʹ��
��ʹ��![]() �cƽ��
�cƽ��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��![]() .
.


 �S����܊�n�n��ϵ�д�
�S����܊�n�n��ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���x��4��4������(bi��o)ϵ�c����(sh��)����
��ƽ��ֱ������(bi��o)ϵ![]() �У�ֱ��
�У�ֱ��![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�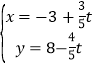 ��
��![]() �酢��(sh��)�����A
�酢��(sh��)�����A![]() �ķ��̞�
�ķ��̞�![]() ����ԭ�c(di��n)
����ԭ�c(di��n)![]() ��O�c(di��n)��
��O�c(di��n)��![]() �S�����S��O�S�����O����(bi��o)ϵ��
�S�����S��O�S�����O����(bi��o)ϵ��
������ֱ��![]() ���A
���A![]() �ĘO����(bi��o)���̣�
�ĘO����(bi��o)���̣�
������ֱ��![]() �c�A
�c�A![]() ����
����![]() ��
��![]() ���c(di��n)����
���c(di��n)����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵxOy�У���֪����C�ą���(sh��)���̞�![]() �����酢��(sh��)��ֱ��l��y=kx��k��0������O��O�c(di��n)��x�S�����S��O�S�����O����(bi��o)ϵ��
�����酢��(sh��)��ֱ��l��y=kx��k��0������O��O�c(di��n)��x�S�����S��O�S�����O����(bi��o)ϵ��
����������C�ĘO����(bi��o)���̣�
������ֱ��l�c����C����A��B���c(di��n)����|OA||OB|��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪���タ![]() �Ľ��c(di��n)��
�Ľ��c(di��n)��![]() ��
��![]() ��
��![]() �ǒ��タ�ϵăɂ�(g��)��(d��ng)�c(di��n)����
�ǒ��タ�ϵăɂ�(g��)��(d��ng)�c(di��n)����![]() ���^
���^![]() ��
��![]() ���c(di��n)�քe�����タ���о����O(sh��)�佻�c(di��n)��
���c(di��n)�քe�����タ���о����O(sh��)�佻�c(di��n)��![]() .
.
��1����ֱ��![]() �c
�c![]() ��
��![]() �S�քe�����c(di��n)
�S�քe�����c(di��n)![]() ��
��![]() ����
����![]() ����e��
����e��![]() ����
����![]() ��ֵ��
��ֵ��
��2��ӛ![]() ����e��
����e��![]() ����
����![]() ����Сֵ����ָ��
����Сֵ����ָ��![]() ��С�r(sh��)����(y��ng)���c(di��n)
���r(sh��)����(y��ng)���c(di��n)![]() ������(bi��o).
������(bi��o).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���x��4-4������(bi��o)ϵ�c����(sh��)����
��ƽ��ֱ������(bi��o)ϵ![]() �У�ֱ��
�У�ֱ��![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�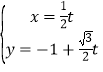 ��
��![]() �酢��(sh��)����������(bi��o)ԭ�c(di��n)
�酢��(sh��)����������(bi��o)ԭ�c(di��n)![]() ��O�c(di��n)����
��O�c(di��n)����![]() �S�����S��O�S�������O����(bi��o)ϵ������
�S�����S��O�S�������O����(bi��o)ϵ������![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() .
.
��1����ֱ��![]() ����ͨ���̺�����
����ͨ���̺�����![]() ��ֱ������(bi��o)���̣�
��ֱ������(bi��o)���̣�
��2����ֱ��![]() �c����
�c����![]() �ཻ��
�ཻ��![]() ���c(di��n)���O(sh��)�c(di��n)
���c(di��n)���O(sh��)�c(di��n)![]() ����֪
����֪![]() ����(sh��)��(sh��)
����(sh��)��(sh��)![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�c(di��n)A,B,C,D��ֱ������(bi��o)ϵ�в�ͬ�����c(di��n)����![]() ��
��![]() ����
����![]() ���t�����f�����_����( ),
���t�����f�����_����( ),
A.C�����Ǿ���AB�����c(di��n)
B.D�����Ǿ���AB�����c(di��n)
C.C��D����ͬ�r(sh��)�ھ���AB��
D.C��D������ͬ�r(sh��)�ھ���AB�����L����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�ɂ�(g��)ƽ�����ֱ���������}
��һ��(g��)ƽ���(n��i)��ֱ֪���ش�ֱ����һ��(g��)ƽ���(n��i)������һ�lֱ��
��һ��(g��)ƽ���(n��i)��ֱ֪���ش�ֱ����һ��(g��)ƽ���(n��i)�ğo��(sh��)�lֱ��
��һ��(g��)ƽ���(n��i)����һ�lֱ���ش�ֱ����һ��(g��)ƽ��
���^һ��(g��)ƽ���(n��i)����һ�c(di��n)�������Ĵ������t�˴����ش�ֱ����һ��(g��)ƽ��
�������_���}��(g��)��(sh��)�ǣ� ��
A. ![]() B.
B. ![]() C. 1D.
C. 1D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���|���̵���ُ�M(j��n)ij�NʳƷ�����|(zh��)��һ�죩�����̵�ÿ����ُ�M(j��n)ԓʳƷһ�Σ�ُ�M(j��n)�r(sh��)��ԓʳƷ�鄂���a(ch��n)�ģ�.����(j��)�Ј��{(di��o)�飬ԓʳƷÿ���M(j��n)�r(ji��)![]() Ԫ���ۃr(ji��)
Ԫ���ۃr(ji��)![]() Ԫ�����һ���(n��i)�o���۳����tʳƷ�^�����U���F(xi��n)�y(t��ng)Ӌ(j��)ԓ�a(ch��n)Ʒ
Ԫ�����һ���(n��i)�o���۳����tʳƷ�^�����U���F(xi��n)�y(t��ng)Ӌ(j��)ԓ�a(ch��n)Ʒ![]() ����N�������±���
����N�������±���

��1������(j��)ԓ�a(ch��n)Ʒ![]() ����N�����y(t��ng)Ӌ(j��)������ƽ��ÿ���N�۶��ٷݣ�
����N�����y(t��ng)Ӌ(j��)������ƽ��ÿ���N�۶��ٷݣ�
��2��ҕ�ӱ��l�ʞ���ʣ���һ���(n��i)ԓ�a(ch��n)Ʒ���@�õ�������ƽ��ֵ��Q������(j��)���|���̵�һ����ُ�M(j��n)![]() ��
��![]() �ݣ���һ�N�õ�����������
�ݣ���һ�N�õ�����������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe��![]() ���ҙE�A�ϴ���һ�c(di��n)
���ҙE�A�ϴ���һ�c(di��n)![]() ���M��
���M��![]() .
.
��1����E�A![]() �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2���^�E�A![]() �ҽ��c(di��n)
�ҽ��c(di��n)![]() ��ֱ��
��ֱ��![]() �c�E�A
�c�E�A![]() ���ڲ�ͬ�ă��c(di��n)
���ڲ�ͬ�ă��c(di��n)![]() ����
����![]() �ă�(n��i)�ЈA�İ돽�����ֵ.
�ă�(n��i)�ЈA�İ돽�����ֵ.
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com