Question

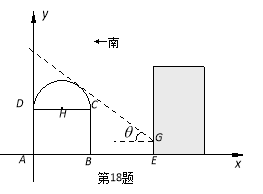
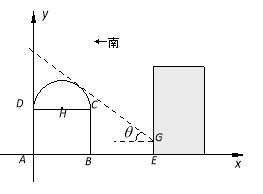
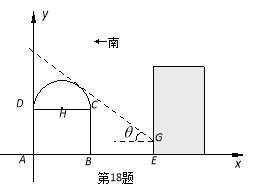
【題目】如圖所示，某街道居委會擬在地段的居民樓正南方向的空白地段上建一個活動中心，其中米．活動中心東西走向，與居民樓平行. 從東向西看活動中心的截面圖的下部分是長方形，上部分是以為直徑的半圓. 為了保證居民樓住戶的采光要求，活動中心在與半圓相切的太陽光線照射下落在居民樓上的影長不超過米，其中該太陽光線與水平線的夾角滿足.

（1）若設計米，米，問能否保證上述采光要求？

（2）在保證上述采光要求的前提下，如何設計與的長度，可使得活動中心的截面面積最大？（注：計算中取3）

Answer 1

【答案】（Ⅰ）能（Ⅱ）米且米

【解析】

試題分析：（Ⅰ）由條件知研究直線與圓相切，所以建立坐標系：以點A為坐標原點，AB所在直線為x軸，，確定圓的方程，求出切線方程，解出切線與直線交點，最后判斷是否滿足不超過米這個條件（Ⅱ）同（1）建立坐標系，設立圓的方程：圓心為，半徑為，求出切線方程，解出切線與直線交點，根據 不超過米這個條件列參數限制條件，最后根據活動中心的截面面積關系式求最值：

試題解析：解：如圖所示，以點A為坐標原點，AB所在直線為x軸，建立平面直角坐標系．

（1）因為，，所以半圓的圓心為，

半徑．設太陽光線所在直線方程為，

即， ...............2分

則由，

解得或（舍）.

故太陽光線所在直線方程為， ...............5分

令，得米米.

所以此時能保證上述采光要求. ...............7分

（2）設米，米，則半圓的圓心為，半徑為．

方法一：設太陽光線所在直線方程為，

即，由，

解得或（舍）. ...............9分

故太陽光線所在直線方程為，

令，得，由，得. ...............11分

所以

.

當且僅當時取等號.

所以當米且米時，可使得活動中心的截面面積最大. .............16分

方法二：欲使活動中心內部空間盡可能大，則影長EG恰為米，則此時點為，

設過點G的上述太陽光線為，則所在直線方程為y－＝－(x－30)，

即． ........10分

由直線與半圓H相切，得．

而點H(r，h)在直線的下方，則3r＋4h－100＜0，

即，從而． ...............13分

又.

當且僅當時取等號.

所以當米且米時，可使得活動中心的截面面積最大. ...........16分