
【題目】如圖,將邊長為2的正方形ABCD沿PD、PC翻折至A、B兩點(diǎn)重合,其中P是AB中點(diǎn),在折成的三棱錐A(B)-PDC中,點(diǎn)Q在平面PDC內(nèi)運(yùn)動(dòng),且直線AQ與棱AP所成角為60,則點(diǎn)Q運(yùn)動(dòng)的軌跡是
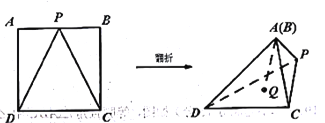
A. 圓 B. 橢圓 C. 雙曲線 D. 拋物線
【答案】D
【解析】
建立空間坐標(biāo)系,設(shè)![]() ,求出點(diǎn)
,求出點(diǎn)![]() 的坐標(biāo),由直線AQ與棱AP所成角為60,利用空間向量夾角公式列方程,得到關(guān)于
的坐標(biāo),由直線AQ與棱AP所成角為60,利用空間向量夾角公式列方程,得到關(guān)于![]() 的方程,從方程的形式可判斷Q點(diǎn)的軌跡。
的方程,從方程的形式可判斷Q點(diǎn)的軌跡。
如圖,過點(diǎn)A引平面PDC的垂線,垂足為O,以O為坐標(biāo)原點(diǎn)建立空間直角坐標(biāo)系,其中![]() 軸與直線DC平行,點(diǎn)P在
軸與直線DC平行,點(diǎn)P在![]() 軸的負(fù)半軸上。
軸的負(fù)半軸上。
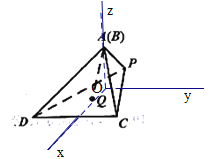
由題可知PA![]() 平面ADC,又
平面ADC,又![]() ,求得點(diǎn)A到平面PCD的距離為:
,求得點(diǎn)A到平面PCD的距離為:![]() ,所以
,所以![]() ,
,![]() ,設(shè)
,設(shè)![]() ,
,
所以![]() ,
,![]() ,又直線AQ與棱AP所成角為60,所以
,又直線AQ與棱AP所成角為60,所以 ,整理得:
,整理得:![]() ,所以點(diǎn)Q的軌跡為拋物線.故選D。
,所以點(diǎn)Q的軌跡為拋物線.故選D。



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】將下列問題的解答過程補(bǔ)充完整.
依次計(jì)算數(shù)列![]() ,
,![]() ,
,![]() ,
,![]() ,…的前四項(xiàng)的值,由此猜測
,…的前四項(xiàng)的值,由此猜測![]() 的有限項(xiàng)的表達(dá)式,并用數(shù)學(xué)歸納法加以證明.
的有限項(xiàng)的表達(dá)式,并用數(shù)學(xué)歸納法加以證明.
解:計(jì)算 ![]() ,
,
![]() ,
,
![]() ① ,
① ,
![]() ② ,
② ,
由此猜想![]() ③ .(*)
③ .(*)
下面用數(shù)學(xué)歸納法證明這一猜想.
(i)當(dāng)![]() 時(shí),左邊
時(shí),左邊![]() ,右邊
,右邊![]() ,所以等式成立.
,所以等式成立.
(ⅱ)假設(shè)當(dāng)![]() 時(shí),等式成立,即
時(shí),等式成立,即
![]() ④ .
④ .
那么,當(dāng)![]() 時(shí),
時(shí),
![]() ⑤
⑤
![]() ⑥
⑥
![]() ⑦ .
⑦ .
等式也成立.
根據(jù)(i)和(ⅱ)可以斷定,(*)式對任何![]() 都成立.
都成立.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若曲線![]() 和
和![]() 上分別存在點(diǎn)
上分別存在點(diǎn)![]() ,使得
,使得![]() 是以原點(diǎn)
是以原點(diǎn)![]() 為直角頂點(diǎn)的直角三角形,AB交y軸于C,且
為直角頂點(diǎn)的直角三角形,AB交y軸于C,且![]() 則實(shí)數(shù)
則實(shí)數(shù)![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)若曲線![]() 在
在![]() 處的切線方程為
處的切線方程為![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的值;
的值;
(2)設(shè)![]() ,若對任意兩個(gè)不等的正數(shù)
,若對任意兩個(gè)不等的正數(shù)![]() ,
,![]() ,都有
,都有![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(3)若在![]() 上存在一點(diǎn)
上存在一點(diǎn)![]() ,使得
,使得![]() 成立,求實(shí)數(shù)
成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某商場為了了解顧客的購物信息,隨機(jī)在商場收集了![]() 位顧客購物的相關(guān)數(shù)據(jù)如下表:
位顧客購物的相關(guān)數(shù)據(jù)如下表:
一次購物款(單位:元) |
|
|
|
|
|
顧客人數(shù) |
|
|
|
|
|
統(tǒng)計(jì)結(jié)果顯示![]() 位顧客中購物款不低于
位顧客中購物款不低于![]() 元的顧客占
元的顧客占![]() ,該商場每日大約有
,該商場每日大約有![]() 名顧客,為了增加商場銷售額度,對一次購物不低于
名顧客,為了增加商場銷售額度,對一次購物不低于![]() 元的顧客發(fā)放紀(jì)念品.
元的顧客發(fā)放紀(jì)念品.
(Ⅰ)試確定![]() ,
, ![]() 的值,并估計(jì)每日應(yīng)準(zhǔn)備紀(jì)念品的數(shù)量;
的值,并估計(jì)每日應(yīng)準(zhǔn)備紀(jì)念品的數(shù)量;
(Ⅱ)現(xiàn)有![]() 人前去該商場購物,求獲得紀(jì)念品的數(shù)量
人前去該商場購物,求獲得紀(jì)念品的數(shù)量![]() 的分布列與數(shù)學(xué)期望.
的分布列與數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列說法正確的是( )
A.甲、乙兩人做游戲:甲、乙兩人各寫一個(gè)數(shù)字,若都是奇數(shù)或都是偶數(shù)則甲勝,否則乙勝,這個(gè)游戲公平
B.做![]() 次隨機(jī)試驗(yàn),事件
次隨機(jī)試驗(yàn),事件![]() 發(fā)生的頻率就是事件
發(fā)生的頻率就是事件![]() 發(fā)生的概率
發(fā)生的概率
C.某地發(fā)行福利彩票,回報(bào)率為47%,某人花了100元買該福利彩票,一定會(huì)有47元的回報(bào)
D.有甲、乙兩種報(bào)紙可供某人訂閱,事件![]() “某人訂閱甲報(bào)紙”是必然事件
“某人訂閱甲報(bào)紙”是必然事件
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對于定義域?yàn)?/span>D的函數(shù)f(x),若存在區(qū)間[m,n]![]() D,同時(shí)滿足下列條件:①f(x)在[m,n]上是單調(diào)的;②當(dāng)定義域是[m,n]時(shí),f(x)的值域也是[m,n],則稱[m,n]為該函數(shù)的“和諧區(qū)間”.下列函數(shù)存在“和諧區(qū)間”的有( )
D,同時(shí)滿足下列條件:①f(x)在[m,n]上是單調(diào)的;②當(dāng)定義域是[m,n]時(shí),f(x)的值域也是[m,n],則稱[m,n]為該函數(shù)的“和諧區(qū)間”.下列函數(shù)存在“和諧區(qū)間”的有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() ,直線
,直線![]() 與函數(shù)
與函數(shù)![]() 的圖象在
的圖象在![]() 處相切,設(shè)
處相切,設(shè)![]() ,若在區(qū)間[1,2]上,不等式
,若在區(qū)間[1,2]上,不等式![]() 恒成立.則實(shí)數(shù)m( )
恒成立.則實(shí)數(shù)m( )
A. 有最大值![]() B. 有最大值e C. 有最小值e D. 有最小值
B. 有最大值e C. 有最小值e D. 有最小值![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)點(diǎn)P,Q分別是曲線y=xe﹣x(e是自然對數(shù)的底數(shù))和直線y=x+3上的動(dòng)點(diǎn),則P,Q兩點(diǎn)間距離的最小值為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com