
【題目】函數 ![]() .
.
(1)求函數 ![]() 的最小正周期;
的最小正周期;
(2)在 ![]() 中,
中, ![]() 分別為內角
分別為內角 ![]() 的對邊,且
的對邊,且 ![]() ,
, ![]() ,求
,求 ![]() 的面積的最大值.
的面積的最大值.
【答案】
(1)解: ![]() ,
,
所以最小正周期為 ![]() .
.
(2)解: ![]()
![]() ,
,
由 ![]() 得到
得到 ![]() ,所以
,所以 ![]() ,所以
,所以 ![]() ,
,
所以 ![]() ,由于
,由于 ![]() ,所以
,所以 ![]() ,
,
解得 ![]() ,
, ![]() 取等號,所以
取等號,所以 ![]() 的面積的最大值為
的面積的最大值為 ![]() .
.
【解析】(1)利用二倍角公式化簡原函數得到關于x的正弦型函數,根據正弦函數的周期公式求出即可。(2)利用三角形的面積公式結合同意可求出角A的值,再由余弦定理可求得 b2 + c2= 4 + b c,利用基本不等式可求出 b c ≤ 4 ,進而可得到△ A B C 的面積的最大值。
【考點精析】掌握基本不等式在最值問題中的應用和二倍角的余弦公式是解答本題的根本,需要知道用基本不等式求最值時(積定和最小,和定積最大),要注意滿足三個條件“一正、二定、三相等”;二倍角的余弦公式:![]() .
.


科目:高中數學 來源: 題型:
【題目】某種水果的單個質量在500g以上視為特等品.隨機抽取1000個該水果,結果有50個特等品.將這50個水果的質量數據分組,得到下邊的頻率分布表.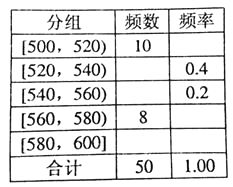
(1)估計該水果的質量不少于560g的概率;
(2)若在某批水果的檢測中,發現有15個特等品,據此估計該批水果中沒有達到特等品的個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列四個命題:
①函數![]() 的一條對稱軸是
的一條對稱軸是![]()
②函數![]() 的圖像關于點
的圖像關于點![]() 對稱;
對稱;
③正弦函數在第一象限為增函數;
④若![]() ,則
,則![]() 其中
其中![]()
其中正確的有____________.(填寫正確命題前面的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】拖延癥總是表現在各種小事上,但日積月累,特別影響個人發展.某校的一個社會實踐調查小組,在對該校學生進行“是否有明顯拖延癥”的調查中,隨機發放了110份問卷.對收回的100份有效問卷進行統計,得到如下 ![]() 列聯表:
列聯表:
(1)按女生是否有明顯拖延癥進行分層,已經從40份女生問卷中抽取了8份問卷,現從這8份問卷中再隨機抽取3份,并記其中無明顯拖延癥的問卷的份數為 ![]() ,試求隨機變量
,試求隨機變量 ![]() 的分布列和數學期望;
的分布列和數學期望;
(2)若在犯錯誤的概率不超過 ![]() 的前提下認為無明顯拖延癥與性別有關,那么根據臨界值表,最精確的
的前提下認為無明顯拖延癥與性別有關,那么根據臨界值表,最精確的 ![]() 的值應為多少?請說明理由.附:獨立性檢驗統計量
的值應為多少?請說明理由.附:獨立性檢驗統計量 ![]() ,其中
,其中 ![]() .
.
獨立性檢驗臨界值表:
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個正四面體的“骰子”(四個面分別標有1,2,3,4四個數字),擲一次“骰子”三個側面的數字的和為“點數”,連續拋擲“骰子”兩次.
(1)設A為事件“兩次擲‘骰子’的點數和為16”,求事件A發生的概率;
(2)設X為兩次擲“骰子”的點數之差的絕對值,求隨機變量X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以直角坐標系的原點O為極點,x軸的正半軸為極軸建立極坐標系,已知點P的直角坐標為(1,2),點M的極坐標為 ![]() ,若直線l過點P,且傾斜角為
,若直線l過點P,且傾斜角為 ![]() ,圓C以M為圓心,3為半徑.
,圓C以M為圓心,3為半徑.
(Ⅰ)求直線l的參數方程和圓C的極坐標方程;
(Ⅱ)設直線l與圓C相交于A,B兩點,求|PA||PB|.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面直角坐標系中,直線l的參數方程是![]() (t為參數),以坐標原點為極點,x軸的正半軸為極軸,建立極坐標系,已知曲線C的極坐標方程為ρ2cos2θ+ρ2sin2θ﹣2ρsinθ﹣3=0.
(t為參數),以坐標原點為極點,x軸的正半軸為極軸,建立極坐標系,已知曲線C的極坐標方程為ρ2cos2θ+ρ2sin2θ﹣2ρsinθ﹣3=0.
(1)求直線l的極坐標方程;
(2)若直線l與曲線C相交于A、B兩點,求|AB|.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)兩個共軛復數的差是純虛數;(2)兩個共軛復數的和不一定是實數;(3)若復數a+bi(a,b∈R)是某一元二次方程的根,則a﹣bi是也一定是這個方程的根;(4)若z為虛數,則z的平方根為虛數,
其中正確的個數為( )
A.3
B.2
C.1
D.0
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com