
【題目】數學家歐拉在1765年提出,任意三角形的外心、重心、垂心位于同一條直線上,后人稱這條直線為歐拉線.已知△ABC的頂點A(2,0),B(0,4),若其歐拉線的方程為x-y+2=0,則頂點C的坐標為
A. (-4,0) B. (-3,-1) C. (-5,0) D. (-4,-2)
【答案】A
【解析】
設點的坐標為C(m,n),由重心公式得到關于m,n的方程,然后利用外心與點B的距離與外心與點C的距離相等得到關于m,n的方程,兩方程聯立即可確定頂點C的坐標.
設C(m,n),由重心公式,可得△ABC的重心為![]() ,
,
代入歐拉直線有:![]() ,
,
整理得m-n+4=0 ①.
AB的中點為(1,2),kAB=![]() =-2,
=-2,
AB的中垂線方程為y-2=![]() (x-1),即x-2y+3=0,
(x-1),即x-2y+3=0,
聯立![]() 可得:
可得:![]() ,所以△ABC的外心為(-1,1),
,所以△ABC的外心為(-1,1),
外心與點B的距離:![]() ,
,
外心與點B的距離與外心與點C的距離相等,則:
(m+1)2+(n-1)2=10,整理得m2+n2+2m-2n=8 ②,
聯立①②,可得m=-4,n=0或m=0,n=4.
當m=0,n=4時,B,C兩點重合,舍去,
當m=-4,n=0時滿足題意.
所以點C的坐標為(-4,0).
本題選擇A選項.


科目:高中數學 來源: 題型:
【題目】人的眼皮有單眼皮與雙眼皮之分,這是由對應的基因決定的.生物學上已經證明:決定眼皮單雙的基因有兩種,一種是顯性基因(記為![]() ),另一種是隱性基因(記為
),另一種是隱性基因(記為![]() );基因總是成對出現(如
);基因總是成對出現(如![]() 、
、![]() 、
、![]() 、
、![]() ),而成對的基因中,只要出現了顯性基因,那么這個人就一定是雙眼皮(也就是說,“單眼皮”的充要條件是“成對的基因是
),而成對的基因中,只要出現了顯性基因,那么這個人就一定是雙眼皮(也就是說,“單眼皮”的充要條件是“成對的基因是![]() ”);如果不發生基因突變的話,成對的基因中,一個來自父親,另一個來自母親,但父母親提供基因時都是隨機的.有一對夫妻,兩人成對的基因都是
”);如果不發生基因突變的話,成對的基因中,一個來自父親,另一個來自母親,但父母親提供基因時都是隨機的.有一對夫妻,兩人成對的基因都是![]() ,不考慮基因突變,求他們的孩子是單眼皮的概率.
,不考慮基因突變,求他們的孩子是單眼皮的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
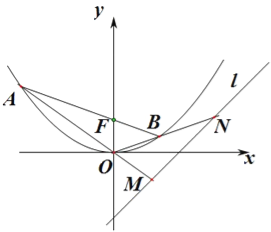
【題目】已知拋物線C的頂點為O(0,0),焦點F(0,1)
(Ⅰ)求拋物線C的方程;
(Ⅱ)過F作直線交拋物線于A、B兩點.若直線OA、OB分別交直線l:y=x﹣2于M、N兩點,求|MN|的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】袋中有紅、白球各一個,每次任取一個,有放回地摸三次,求基本事件的個數n,寫出所有基本事件的全集I,并計算下列事件的概率:
(1)三次顏色恰有兩次同色;
(2)三次顏色全相同;
(3)三次摸到的紅球多于白球.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在對人們的休閑方式的一次調查中,共調查了110人,其中女性50人,男性60人.女性中有30人主要的休閑方式是看電視,另外20人主要的休閑方式是運動;男性中有20人主要的休閑方式是看電視,另外40人主要的休閑方式是運動.
(1)根據以上數據建立一個2×2列聯表;
(2)判斷性別與休閑方式是否有關系.
下面臨界值表供參考:
P(K2≥k) | 0.10 | 0.05 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
(參考公式:K2=![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
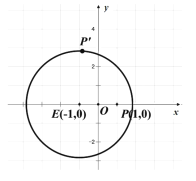
【題目】如圖,一張坐標紙上一已作出圓![]() 及點
及點![]() ,折疊此紙片,使
,折疊此紙片,使![]() 與圓周上某點
與圓周上某點![]() 重合,每次折疊都會留下折痕,設折痕與直線
重合,每次折疊都會留下折痕,設折痕與直線![]() 的交點為
的交點為![]() ,令點
,令點![]() 的軌跡為
的軌跡為![]() .
.
(1)求軌跡![]() 的方程;
的方程;
(2)若直線![]() 與軌跡
與軌跡![]() 交于兩個不同的點
交于兩個不同的點![]() ,且直線
,且直線![]() 與以
與以![]() 為直徑的圓相切,若
為直徑的圓相切,若![]() ,求
,求![]() 的面積的取值范圍.
的面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=loga(![]() )(0<a<1,b>0)為奇函數,當x∈(﹣1,a]時,函數y=f(x)的值域是(﹣∞,1].
)(0<a<1,b>0)為奇函數,當x∈(﹣1,a]時,函數y=f(x)的值域是(﹣∞,1].
(1)確定b的值;
(2)證明函數y=f(x)在定義域上單調遞增,并求a的值;
(3)若對于任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)>0恒成立,求k的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com