
【題目】已知函數![]() .
.
(1)討論![]() 的單調性;
的單調性;
(2)當![]() 時,記
時,記![]() 在區間
在區間![]() 的最大值為
的最大值為![]() ,最小值為
,最小值為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)見詳解;(2) ![]() .
.
【解析】
(1)先求![]() 的導數,再根據
的導數,再根據![]() 的范圍分情況討論函數單調性;(2) 討論
的范圍分情況討論函數單調性;(2) 討論![]() 的范圍,利用函數單調性進行最大值和最小值的判斷,最終求得
的范圍,利用函數單調性進行最大值和最小值的判斷,最終求得![]() 的取值范圍.
的取值范圍.
(1)對![]() 求導得
求導得![]() .所以有
.所以有
當![]() 時,
時,![]() 區間上單調遞增,
區間上單調遞增,![]() 區間上單調遞減,
區間上單調遞減,![]() 區間上單調遞增;
區間上單調遞增;
當![]() 時,
時,![]() 區間上單調遞增;
區間上單調遞增;
當![]() 時,
時,![]() 區間上單調遞增,
區間上單調遞增,![]() 區間上單調遞減,
區間上單調遞減,![]() 區間上單調遞增.
區間上單調遞增.
(2)
若![]() ,
,![]() 在區間
在區間![]() 單調遞減,在區間
單調遞減,在區間![]() 單調遞增,所以區間
單調遞增,所以區間![]() 上最小值為
上最小值為![]() .而
.而![]() ,故所以區間
,故所以區間![]() 上最大值為
上最大值為![]() .
.
所以![]() ,設函數
,設函數![]() ,求導
,求導![]() 當
當![]() 時
時![]() 從而
從而![]() 單調遞減.而
單調遞減.而![]() ,所以
,所以![]() .即
.即![]() 的取值范圍是
的取值范圍是![]() .
.
若![]() ,
,![]() 在區間
在區間![]() 單調遞減,在區間
單調遞減,在區間![]() 單調遞增,所以區間
單調遞增,所以區間![]() 上最小值為
上最小值為![]() 而
而![]() ,故所以區間
,故所以區間![]() 上最大值為
上最大值為![]() .
.
所以![]() ,而
,而![]() ,所以
,所以![]() .即
.即![]() 的取值范圍是
的取值范圍是![]() .
.
綜上得![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左焦點為F,短軸的兩個端點分別為A,B,且
的左焦點為F,短軸的兩個端點分別為A,B,且![]() ,
,![]() 為等邊三角形.
為等邊三角形.

(1)求橢圓C的方程;
(2)如圖,點M在橢圓C上且位于第一象限內,它關于坐標原點O的對稱點為N;過點M作x軸的垂線,垂足為H,直線![]() 與橢圓C交于另一點J,若
與橢圓C交于另一點J,若![]() ,試求以線段
,試求以線段![]() 為直徑的圓的方程;
為直徑的圓的方程;
(3)已知![]() 是過點A的兩條互相垂直的直線,直線
是過點A的兩條互相垂直的直線,直線![]() 與圓
與圓![]() 相交于P,Q兩點,直線
相交于P,Q兩點,直線![]() 與橢圓C交于另一點R,求
與橢圓C交于另一點R,求![]() 面積最大值時,直線
面積最大值時,直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數![]() 和函數
和函數![]() ,
,
(1)若![]() 為偶函數,試判斷
為偶函數,試判斷![]() 的奇偶性;
的奇偶性;
(2)若方程![]() 有兩個不等的實根
有兩個不等的實根![]() ,則
,則
①試判斷函數![]() 在區間
在區間![]() 上是否具有單調性,并說明理由;
上是否具有單調性,并說明理由;
②若方程![]() 的兩實根為
的兩實根為![]() 求使
求使![]() 成立的
成立的![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】第七屆世界軍人運動會于2019年10月18日至2019年10月27日在中國武漢舉行,第七屆世界軍人運動會是我國第一次承辦的綜合性國際軍事體育賽事,也是繼北京奧運會之后我國舉辦的規模最大的國際體育盛會.來自109個國家的9300余名軍體健兒在江城武漢同場競技、增進友誼.運動會共設置射擊、游泳、田徑、籃球等27個大項、329個小項.經過激烈角逐,獎牌榜的前6名如下:
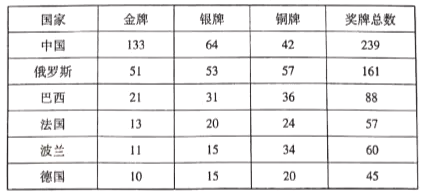
某大學德語系同學利用分層抽樣的方式從德國獲獎選手中抽取了9名獲獎代表.
(1)請問這9名獲獎代表中獲金牌、銀牌、銅牌的人數分別是多少人?
(2)從這9人中隨機抽取3人,記這3人中銀牌選手的人數為![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
(3)從這9人中隨機抽取3人,求已知這3人中有獲金牌運動員的前提下,這3人中恰好有1人為獲銅牌運動員的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 的內切圓與三邊
的內切圓與三邊![]() 的切點分別為
的切點分別為![]() ,已知
,已知![]() ,內切圓圓心
,內切圓圓心![]() ,設點A的軌跡為R.
,設點A的軌跡為R.
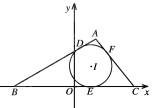
(1)求R的方程;
(2)過點C的動直線m交曲線R于不同的兩點M,N,問在x軸上是否存在一定點Q(Q不與C重合),使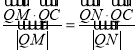 恒成立,若求出Q點的坐標,若不存在,說明理由.
恒成立,若求出Q點的坐標,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC-![]() 中,
中,![]() 平面ABC,D,E,F,G分別為
平面ABC,D,E,F,G分別為![]() ,AC,
,AC,![]() ,
,![]() 的中點,AB=BC=
的中點,AB=BC=![]() ,AC=
,AC=![]() =2.
=2.

(Ⅰ)求證:AC⊥平面BEF;
(Ⅱ)求二面角B-CD-C1的余弦值;
(Ⅲ)證明:直線FG與平面BCD相交.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業新研發了一種產品,產品的成本由原料成本及非原料成本組成.每件產品的非原料成本![]() (元)與生產該產品的數量
(元)與生產該產品的數量![]() (千件)有關,經統計得到如下數據:
(千件)有關,經統計得到如下數據:
![]()
根據以上數據,繪制了散點圖.
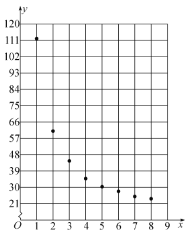
觀察散點圖,兩個變量不具有線性相關關系,現考慮用反比例函數模型![]() 和指數函數模型
和指數函數模型![]() 分別對兩個變量的關系進行擬合.已求得用指數函數模型擬合的回歸方程為
分別對兩個變量的關系進行擬合.已求得用指數函數模型擬合的回歸方程為![]() ,
,![]() 與
與![]() 的相關系數
的相關系數![]() .參考數據(其中
.參考數據(其中![]() ):
):

(1)用反比例函數模型求![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(2)用相關系數判斷上述兩個模型哪一個擬合效果更好(精確到0.01),并用其估計產量為10千件時每件產品的非原料成本;
(3)該企業采取訂單生產模式(根據訂單數量進行生產,即產品全部售出).根據市場調研數據,若該產品單價定為100元,則簽訂9千件訂單的概率為0.8,簽訂10千件訂單的概率為0.2;若單價定為90元,則簽訂10千件訂單的概率為0.3,簽訂11千件訂單的概率為0.7.已知每件產品的原料成本為10元,根據(2)的結果,企業要想獲得更高利潤,產品單價應選擇100元還是90元,請說明理由.
參考公式:對于一組數據![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: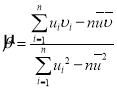 ,
,![]() ,相關系數
,相關系數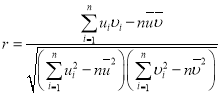 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com