
【題目】已知函數![]() ,其中a為非零常數.
,其中a為非零常數.
![]() 討論
討論![]() 的極值點個數,并說明理由;
的極值點個數,并說明理由;
![]() 若
若![]() ,
,![]() 證明:
證明:![]() 在區間
在區間![]() 內有且僅有1個零點;
內有且僅有1個零點;![]() 設
設![]() 為
為![]() 的極值點,
的極值點,![]() 為
為![]() 的零點且
的零點且![]() ,求證:
,求證:![]() .
.
【答案】(1)見解析;(2)(i)證明見解析;(ii)證明見解析.
【解析】
![]() 先對函數求導,然后結合導數與單調性的關系,對a進行分類討論即可求解函數的單調性,進而可確定極值,
先對函數求導,然后結合導數與單調性的關系,對a進行分類討論即可求解函數的單調性,進而可確定極值,
![]() 轉化為證明
轉化為證明![]() 只有一個零點,結合函數與導數知識可證;
只有一個零點,結合函數與導數知識可證;
![]() 由題意可得,
由題意可得,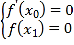 ,代入可得,
,代入可得,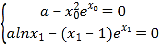 ,結合函數的性質可證.
,結合函數的性質可證.
解:![]() 解:由已知,
解:由已知,![]() 的定義域為
的定義域為![]() ,
,
![]() ,
,
①當![]() 時,
時,![]() ,從而
,從而![]() ,
,
所以![]() 在
在![]() 內單調遞減,無極值點;
內單調遞減,無極值點;
②當![]() 時,令
時,令![]() ,
,
則由于![]() 在
在![]() 上單調遞減,
上單調遞減,![]() ,
,![]() ,
,
所以存在唯一的![]() ,使得
,使得![]() ,
,
所以當![]() 時,
時,![]() ,即
,即![]() ;當
;當![]() 時,
時,![]() ,即
,即![]() ,
,
所以當![]() 時,
時,![]() 在
在![]() 上有且僅有一個極值點.
上有且僅有一個極值點.
綜上所述,當![]() 時,函數
時,函數![]() 無極值點;當
無極值點;當![]() 時,函數
時,函數![]() 只有一個極值點;
只有一個極值點;
![]() 證明:
證明:![]() 由
由![]() 知
知![]() .
.
令![]() ,由
,由![]() 得
得![]() ,
,
所以![]() 在
在![]() 內有唯一解,從而
內有唯一解,從而![]() 在
在![]() 內有唯一解,
內有唯一解,
不妨設為![]() ,則
,則![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,
上單調遞減,
所以![]() 是
是![]() 的唯一極值點.
的唯一極值點.
令![]() ,則當
,則當![]() 時,
時,![]() ,
,
故![]() 在
在![]() 內單調遞減,
內單調遞減,
從而當![]() 時,
時,![]() ,所以
,所以![]() .
.
從而當![]() 時,
時,![]() ,且
,且![]()
又因為![]() ,故
,故![]() 在
在![]() 內有唯一的零點.
內有唯一的零點.
![]() 由題意,
由題意,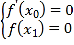 即
即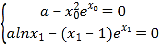 ,
,
從而![]() ,即
,即![]() .
.
因為當![]() 時,
時,![]() ,又
,又![]() ,
,
故![]() ,即
,即![]() ,
,
兩邊取對數,得![]() ,
,
于是![]() ,整理得
,整理得![]() .
.


科目:高中數學 來源: 題型:
【題目】設滿足以下兩個條件的有窮數列![]() 為
為![]() 階“期待數列”:①
階“期待數列”:①![]() ;②
;②![]() .
.
(1)若等比數列![]() 為
為![]() 階“期待數列”
階“期待數列”![]() ,求公比
,求公比![]() ;
;
(2)若一個等差數列![]() 既是
既是![]() 階“期待數列”又是遞增數列
階“期待數列”又是遞增數列![]() ,求該數列的通項公式;
,求該數列的通項公式;
(3)記![]() 階“期待數列”
階“期待數列” ![]() 的前
的前![]() 項和為
項和為![]() ,求證;數列
,求證;數列![]() 不能為
不能為![]() 階“期待數列”.
階“期待數列”.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年11月18日國際射聯步手槍世界杯總決賽在莆田市綜合體育館開幕,這是國際射聯步手槍世界杯總決賽時隔10年再度走進中國.為了增強趣味性,并實時播報現場賽況,我校現場小記者李明和播報小記者王華設計了一套播報轉碼法,發送方由明文→密文(加密),接受方由密文→明文(解密),已知加密的方法是:密碼把英文的明文(真實文)按字母分解,其中英文的![]() 的26個字母(不論大小寫)依次對應1,2,3,…,26這26個自然數通過變換公式:
的26個字母(不論大小寫)依次對應1,2,3,…,26這26個自然數通過變換公式: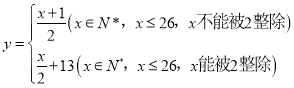 ,將明文轉換成密文,如
,將明文轉換成密文,如![]() ,即
,即![]() 變換成
變換成![]() ,即
,即![]() 變換成
變換成![]() .若按上述規定,若王華收到的密文是
.若按上述規定,若王華收到的密文是![]() ,那么原來的明文是( )
,那么原來的明文是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年1月26日,甘肅省人民政府辦公廳發布《甘肅省關于餐飲業質量安全提升工程的實施意見》,衛生部對16所大學食堂的“進貨渠道合格性”和“食品安全”進行量化評估.滿10分者為“安全食堂”,評分7分以下的為“待改革食堂”.評分在4分以下考慮為“取締食堂”,所有大學食堂的評分在7~10分之間,以下表格記錄了它們的評分情況:

(1)現從16所大學食堂中隨機抽取3個,求至多有1個評分不低于9分的概率;
(2)以這16所大學食堂評分數據估計大學食堂的經營性質,若從全國的大學食堂任選3個,記![]() 表示抽到評分不低于9分的食堂個數,求
表示抽到評分不低于9分的食堂個數,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
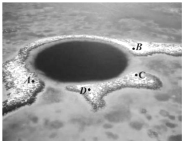
【題目】海洋藍洞是地球罕見的自然地理現象,被喻為“地球留給人類保留宇宙秘密的最后遺產”,我國擁有世界上最深的海洋藍洞,若要測量如圖所示的藍洞的口徑![]() ,
,![]() 兩點間的距離,現在珊瑚群島上取兩點
兩點間的距離,現在珊瑚群島上取兩點![]() ,
,![]() ,測得
,測得![]() ,
,![]() ,
,![]() ,
,![]() ,則
,則![]() ,
,![]() 兩點的距離為___.
兩點的距離為___.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一件剛出土的珍貴文物要在博物館大廳中央展出,需要設計各面是玻璃平面的無底正四棱柱將其罩住,罩內充滿保護文物的無色氣體.已知文物近似于塔形,高1.8米,體積0.5立方米,其底部是直徑為0.9米的圓形,要求文物底部與玻璃罩底邊至少間隔0.3米,文物頂部與玻璃罩上底面至少間隔0.2米,氣體每立方米1000元,則氣體費用最少為( )元

A.4500B.4000C.2880D.2380
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某電視臺舉行一個比賽類型的娛樂節目,A、B兩隊各有六名選手參賽,將他們首輪的比賽成績作為樣本數據,繪制成莖葉圖如圖所示,為了增加節目的趣味性,主持人故意將A隊第六位選手的成績沒有給出,并且告知大家B隊的平均分比A隊的平均分多4分,同時規定如果某位選手的成績不少于21分,則獲得“晉級”.
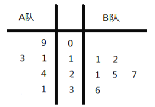
(1)根據莖葉圖中的數據,求出A隊第六位選手的成績;
(2)主持人從A隊所有選手成績中隨機抽取2個,求至少有一個為“晉級”的概率;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com