【題目】已知數列
的前n項和
．
若三角形的三邊長分別為
，
，
，求此三角形的面積；
探究數列中是否存在相鄰的三項，同時滿足以下兩個條件：
此三項可作為三角形三邊的長；
此三項構成的三角形最大角是最小角的2倍
若存在，找出這樣的三項，若不存在，說明理由．
【答案】（1）
（2）見解析
【解析】
數列
的前n項和
求出
，
，遂得出三角形三邊邊長，利用余弦定理求解三角形的面積
假設數列存在相鄰的三項滿足條件，因為，設三角形三邊長分別是n，
，
，
，三個角分別是
，
，
，利用正弦定理，余弦定理，驗證此三角形的最大角是最小角的2倍,然后推出結果．
解：數列的前n項和
．
當
時，
，
當
時，
，
又時，
，所以，
不妨設
三邊長為
，
，
，
所以
所以
假設數列存在相鄰的三項滿足條件，因為，
設三角形三邊長分別是n，，，，三個角分別是，，
由正弦定理：
，所以
由余弦定理：
，
即
化簡得：
，所以：
或
舍去
當時，三角形的三邊長分別是4，5，6，可以驗證此三角形的最大角是最小角的2倍．
所以數列中存在相鄰的三項4，5，6，滿足條件.
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】如圖，O為坐標原點，橢圓C1： 
+ 
=1（a＞b＞0）的左、右焦點分別為F1 ， F2 ， 離心率為e1；雙曲線C2： ﹣ =1的左、右焦點分別為F3 ， F4 ， 離心率為e2 ， 已知e1e2= 
，且|F2F4|= 
﹣1．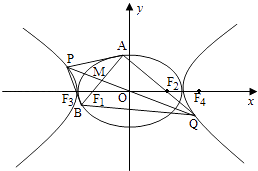 
（1）求C1、C2的方程；
（2）過F1作C1的不垂直于y軸的弦AB，M為AB的中點，當直線OM與C2交于P，Q兩點時，求四邊形APBQ面積的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】計劃在某水庫建一座至多安裝3臺發電機的水電站，過去50年的水文資料顯示，水庫年入流量X（年入流量：一年內上游來水與庫區降水之和．單位：億立方米）都在40以上，其中，不足80的年份有10年，不低于80且不超過120的年份有35年，超過120的年份有5年，將年入流量在以上三段的頻率作為相應段的概率，假設各年的年入流量相互獨立．
（1）求未來4年中，至多有1年的年入流量超過120的概率；
（2）水電站希望安裝的發電機盡可能運行，但每年發電機最多可運行臺數受年入流量X限制，并有如下關系：
年入流量X | 40＜X＜80 | 80≤X≤120 | X＞120 |
發電機最多可運行臺數 | 1 | 2 | 3 |
若某臺發電機運行，則該臺年利潤為5000萬元，若某臺發電機未運行，則該臺年虧損800萬元，欲使水電站年總利潤的均值達到最大，應安裝發電機多少臺？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點p(1,m)在拋物線
上，F為焦點，且
.
（1）求拋物線C的方程；
（2）過點T(4,0)的直線
交拋物線C于A,B兩點，O為坐標原點，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
.
（1）若
， 
都是從0，1，2，3，4五個數中任取的一個數，求上述函數有零點的概率；
（2）若
， 
都是從區間
上任取的一個數，求
成立的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點A（2，0），拋物線C：x2=4y的焦點為F，射線FA與拋物線C相交于點M，與其準線相交于點N，則|FM|：|MN|=________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設數列{an}的前n項和為Sn ， 滿足Sn=2nan+1﹣3n2﹣4n，n∈N* ， 且S3=15．
（1）求a1 ， a2 ， a3的值；
（2）求數列{an}的通項公式．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列說法中正確的是
A. 先把高三年級的2000名學生編號：1到2000，再從編號為1到50的50名學生中隨機抽取1名學生，其編號為
，然后抽取編號為
的學生，這樣的抽樣方法是分層抽樣法
B. 線性回歸直線
不一定過樣本中心點
C. 若兩個隨機變量的線性相關性越強，則相關系數
的值越接近于1
D. 若一組數據1、
、3的平均數是2，則該組數據的方差是
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=xcosx﹣sinx，x∈[0， 
]
（1）求證：f（x）≤0；
（2）若a＜ 
＜b對x∈（0， ）上恒成立，求a的最大值與b的最小值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com