【題目】已知三棱柱
，平面
截此三棱柱，分別與
， 
， 
， 
交于點(diǎn)
， 
， 
， 
，且直線(xiàn)
平面
.有下列三個(gè)命題：①四邊形
是平行四邊形；②平面
平面
；③若三棱柱
是直棱柱，則平面
平面
.其中正確的命題為（ ）
A. ①② B. ①③ C. ①②③ D. ②③
【答案】B
【解析】分析：在①中，由
，且
，即可證明四邊形
是平行四邊形；在②中，由直線(xiàn)
與
的位置關(guān)系可判斷平面
與平面
平行或相交；在③中，若三棱柱
是直棱柱，則
平面
，結(jié)合①，即可得證.
詳解：在三棱柱
中，平面
截此三棱柱，分別與
， 
， 
， 
交于點(diǎn)
， 
， 
， 
，且直線(xiàn)
平面
，則
，且
，所以四邊形
是平行四邊形，故①正確；
∵
與
不一定平行
∴平面
與平面
平行或相交，故②錯(cuò)誤；
若三棱柱
是直棱柱，則
平面
.
∴
平面
又∵
平面
∴平面
平面
，故③正確.
故選B.
名校課堂系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】已知圓
與直線(xiàn)
，動(dòng)直線(xiàn)
過(guò)定點(diǎn)
.
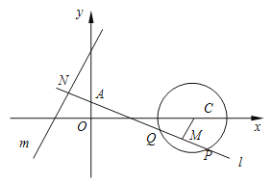
（1）若直線(xiàn)與圓
相切，求直線(xiàn)的方程；
（2）若直線(xiàn)與圓相交于
兩點(diǎn)，點(diǎn)
是
的中點(diǎn)，直線(xiàn)與直線(xiàn)
相交于點(diǎn)
. 探索
是否為定值，若是，求出該定值；若不是，請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】《中國(guó)青年報(bào)》2015年5月14日?qǐng)?bào)道：“伴隨著網(wǎng)絡(luò)技術(shù)的蓬勃發(fā)展，國(guó)內(nèi)電子商務(wù)獲得了爆炸式的增長(zhǎng)，2014年網(wǎng)上零售額達(dá)到了27898億元，占社會(huì)消費(fèi)品零售總額的10%，也就是說(shuō)，人們?nèi)粘ＯM(fèi)中10%是通過(guò)網(wǎng)購(gòu)，而且還以年30%，40%的速度增長(zhǎng)."假設(shè)2014-2020年網(wǎng)上零售額每年的增長(zhǎng)率均為35%，試算出2015-2020年每年的網(wǎng)上零售額（精確到1億元）.
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】某商場(chǎng)在促銷(xiāo)期間規(guī)定：商場(chǎng)內(nèi)所有商品按標(biāo)價(jià)的
出售，當(dāng)顧客在商場(chǎng)內(nèi)消費(fèi)一定金額后，按如下方案獲得相應(yīng)金額的獎(jiǎng)券：
消費(fèi)金額（元）的范圍 |
|
|
|
| … |
獲得獎(jiǎng)券的金額（元） | 30 | 60 | 100 | 130 | … |
根據(jù)上述促銷(xiāo)方法，顧客在該商場(chǎng)購(gòu)物可以獲得雙重優(yōu)惠，例如：購(gòu)買(mǎi)標(biāo)價(jià)為400元的商品，則消費(fèi)金額為320元，獲得的優(yōu)惠額為：
元，設(shè)購(gòu)買(mǎi)商品得到的優(yōu)惠率＝（購(gòu)買(mǎi)商品獲得的優(yōu)惠額）/（商品標(biāo)價(jià)），試問(wèn)：
（1）若購(gòu)買(mǎi)一件標(biāo)價(jià)為1000元的商品，顧客得到的優(yōu)惠率是多少？
（2）對(duì)于標(biāo)價(jià)在
（元）內(nèi)的商品，顧客購(gòu)買(mǎi)標(biāo)價(jià)為多少元的商品，可得到不小于
的優(yōu)惠率？
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】在平面直角坐標(biāo)系
中，以原點(diǎn)
為極點(diǎn)，
軸的非負(fù)半軸為極軸建立極坐標(biāo)系.已知曲線(xiàn)
的極坐標(biāo)方程為
，
為曲線(xiàn)上的動(dòng)點(diǎn)，與軸、
軸的正半軸分別交于
，
兩點(diǎn).
（1）求線(xiàn)段
中點(diǎn)
的軌跡的參數(shù)方程；
（2）若
是（1）中點(diǎn)的軌跡上的動(dòng)點(diǎn)，求
面積的最大值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】在如圖所示的幾何體中，四邊形
為正方形，四邊形
為直角梯形，且
， 
，平面
平面
， 
．
（
）求證： 
平面
．
（
）若二面角
為直二面角，
（i）求直線(xiàn)
與平面
所成角的大小．
（ii）棱
上是否存在點(diǎn)
，使得
平面
？若存在，求出
的值；若不存在，請(qǐng)說(shuō)明理由．
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】如圖，四邊形
是正方形， 
平面
， 
// 
， 
， 
， 
為
的中點(diǎn)．
（1）求證： 
；
（2）求證： 
//平面
；
（3）求二面角
的大小．
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】如圖1，在△
中，
，
分別為
，
的中點(diǎn)，
為
的中點(diǎn)，
，
．將△
沿折起到△
的位置，使得平面
平面
，如圖2．
（Ⅰ）求證：
；
（Ⅱ）求直線(xiàn)
和平面
所成角的正弦值；
（Ⅲ）線(xiàn)段上是否存在點(diǎn)
，使得直線(xiàn)
和
所成角的余弦值為
？若存在，求出
的值；若不存在，說(shuō)明理由．
圖1 圖2
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
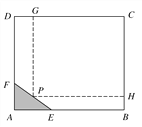
【題目】如圖所示，為了保護(hù)環(huán)境，實(shí)現(xiàn)城市綠化，某房地產(chǎn)公司要在拆遷地長(zhǎng)方形ABCD處規(guī)劃一塊長(zhǎng)方形地面HPGC，建造住宅小區(qū)公園，但不能越過(guò)文物保護(hù)區(qū)三角形AEF的邊線(xiàn)EF.已知AB＝CD＝200 m，BC＝AD＝160 m，AF＝40 m，AE＝60 m，問(wèn)如何設(shè)計(jì)才能使公園占地面積最大，求出最大面積．
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà)：027-86699610 舉報(bào)郵箱：58377363@163.com
