
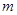 的取值組成的集合
的取值組成的集合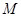 ,使當
,使當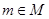 時,“
時,“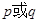 ”為真,“
”為真,“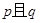 ”為假.
”為假.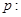 方程
方程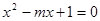 有兩個不相等的負根;
有兩個不相等的負根;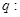 方程
方程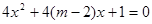 無實數(shù)根.
無實數(shù)根. 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源:不詳 題型:解答題
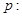 函數(shù)
函數(shù)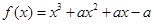 既有極大值又有極小值;
既有極大值又有極小值;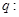 直線
直線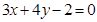 與圓
與圓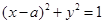 有公共點.
有公共點.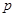 或
或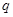 ”為真,且命題“
”為真,且命題“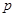 且
且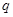 ”為假,試求實數(shù)
”為假,試求實數(shù)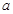 的取值范圍.
的取值范圍.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
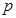 :任意
:任意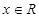 ,
,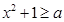 ,命題
,命題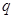 :函數(shù)
:函數(shù)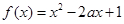 在
在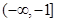 上單調(diào)遞減.
上單調(diào)遞減.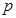 為真命題,求實數(shù)
為真命題,求實數(shù)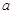 的取值范圍;
的取值范圍;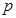 和
和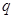 均為真命題,求實數(shù)
均為真命題,求實數(shù)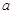 的取值范圍.
的取值范圍.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:填空題
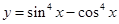 的最小正周期是
的最小正周期是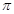 ;
;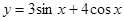 的最大值是
的最大值是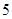 ;
;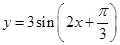 的圖象向右平移
的圖象向右平移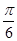 得
得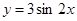 的圖象;
的圖象;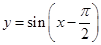 在
在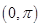 上是減函數(shù).
上是減函數(shù).查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
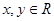 ”,若x
”,若x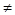 2或y
2或y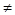 3,則x+y
3,則x+y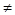 5”是真命題.
5”是真命題.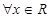 ,ex﹥0”的否定是:“
,ex﹥0”的否定是:“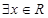 ,ex﹥0”.
,ex﹥0”.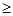 g(x)恒成立的一個充分不必要的條件是f(x)min
g(x)恒成立的一個充分不必要的條件是f(x)min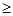 g(x)max.
g(x)max.| A.1 | B.2 | C.3 | D.0 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
 (其中
(其中 為整數(shù)),則
為整數(shù)),則 叫做離實數(shù)
叫做離實數(shù) 最近的整數(shù),記作
最近的整數(shù),記作 ,即
,即 .在此基礎上給出下列關于函數(shù)
.在此基礎上給出下列關于函數(shù) 的四個命題:
的四個命題: 的定義域是
的定義域是 ,值域是
,值域是 ;②點
;②點 是
是 的圖像的對稱中心,其中
的圖像的對稱中心,其中 ;③函數(shù)
;③函數(shù) 的最小正周期為1;④函數(shù)
的最小正周期為1;④函數(shù) 在
在 上是增函數(shù).則上述命題中真命題的序號是( )
上是增函數(shù).則上述命題中真命題的序號是( )| A.①④ | B.①③ | C.②③ | D.②④ |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
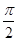 ;命題q:函數(shù)y=cos x的圖象關于直線x=
;命題q:函數(shù)y=cos x的圖象關于直線x=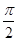 對稱,則下列判斷正確的是( ).
對稱,則下列判斷正確的是( ).| A.p為真 | B.綈q為假 |
| C.p∧q為假 | D.p∨q為真 |
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com