
【題目】已知![]() ,函數
,函數![]()
(1)討論函數![]() 的單調性;
的單調性;
(2)若![]() 是
是![]() 的極值點,且曲線
的極值點,且曲線![]() 在兩點
在兩點![]() ,
,![]()
![]() 處的切線互相平行,這兩條切線在y軸上的截距分別為
處的切線互相平行,這兩條切線在y軸上的截距分別為![]() 、
、![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析;(2)![]()
【解析】
(1)根據導數和函數的關系即可求出函數的單調區間,
(2)由x=2是f(x)的極值點,以及導數的幾何意義,可求出相對應的切線方程,根據切線平行可得![]() ,同理,
,同理,![]() .求出b1﹣b2,再構造函數,
.求出b1﹣b2,再構造函數,
利用導數,即可求出b1﹣b2的取值范圍
(1)![]() ,
,
①當a≤0時,f'(x)<0在x∈(0,+∞)上恒成立,∴f(x)在(0,+∞)上單調遞減;
②當a>0時,![]() 時f'(x)<0,
時f'(x)<0,![]() 時,f'(x)>0,
時,f'(x)>0,
即f(x)在![]() 上單調遞減,在
上單調遞減,在![]() 單調遞增;
單調遞增;
(2)∵x=2是f(x)的極值點,∴由(1)可知![]() ,
,
∴a=1,設在P(x1,f(x1))處的切線方程為![]() ,
,
在Q(x2,f(x2))處的切線方程為![]()
∴若這兩條切線互相平行,則![]() ,∴
,∴![]()
∵![]() ,且0<x1<x2<6,∴
,且0<x1<x2<6,∴![]() ,∴
,∴![]() ,
,
∴x1∈(3,4)令x=0,則![]() ,
,
同理,![]() .
.
【解法一】
∵![]() ,∴
,∴![]()
設![]() ,
,![]()
∴![]()
∴g(x)在區間![]() 上單調遞減,∴
上單調遞減,∴![]()
即b1-b2的取值范圍是![]() .
.
【解法二】
∵![]() ,
,
∴![]()
令![]() ,其中x∈(3,4)
,其中x∈(3,4)
∴![]()
∴函數g(x)在區間(3,4)上單調遞增,∴![]()
∴b1-b2的取值范圍是![]() .
.
【解法三】
∵x1x2=2(x1+x2),
∴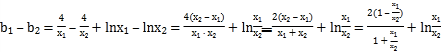
設![]() ,則
,則![]()
∵![]() ,∴g'(x)>0,
,∴g'(x)>0,
∴函數g(x)在區間![]() 上單調遞增,
上單調遞增,
∴![]() ,∴b1-b2的取值范圍是
,∴b1-b2的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】
如圖,長方體ABCD–A1B1C1D1的底面ABCD是正方形,點E在棱AA1上,BE⊥EC1.

(1)證明:BE⊥平面EB1C1;
(2)若AE=A1E,求二面角B–EC–C1的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 的離心率
的離心率![]() ,且圓
,且圓![]() 經過橢圓C的上、下頂點.
經過橢圓C的上、下頂點.
(1)求橢圓C的方程;
(2)若直線l與橢圓C相切,且與橢圓![]() 相交于M,N兩點,證明:
相交于M,N兩點,證明:![]() 的面積為定值(O為坐標原點).
的面積為定值(O為坐標原點).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在菱形![]() 中,
中,![]() ,
,![]() 為線段
為線段![]() 的中點(如圖1).將
的中點(如圖1).將![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,
,![]() 為線段
為線段![]() 的中點(如圖2).
的中點(如圖2).
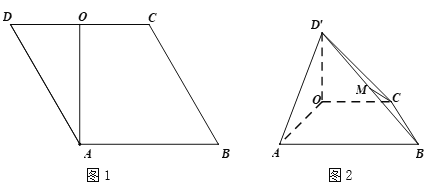
(Ⅰ)求證:![]() ;
;
(Ⅱ)求證:![]() 平面
平面![]() ;
;
(Ⅲ)當四棱錐![]() 的體積為
的體積為![]() 時,求
時,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,直線![]() 與拋物線
與拋物線![]() (常數
(常數![]() )相交于不同的兩點
)相交于不同的兩點![]() 、
、![]() ,且
,且![]() (
(![]() 為定值),線段
為定值),線段![]() 的中點為
的中點為![]() ,與直線
,與直線![]() 平行的切線的切點為
平行的切線的切點為![]() (不與拋物線對稱軸平行或重合且與拋物線只有一個公共點的直線稱為拋物線的切線,這個公共點為切點).
(不與拋物線對稱軸平行或重合且與拋物線只有一個公共點的直線稱為拋物線的切線,這個公共點為切點).

(1)用![]() 、
、![]() 表示出
表示出![]() 點、
點、![]() 點的坐標,并證明
點的坐標,并證明![]() 垂直于
垂直于![]() 軸;
軸;
(2)求![]() 的面積,證明
的面積,證明![]() 的面積與
的面積與![]() 、
、![]() 無關,只與
無關,只與![]() 有關;
有關;
(3)小張所在的興趣小組完成上面兩個小題后,小張連![]() 、
、![]() ,再作與
,再作與![]() 、
、![]() 平行的切線,切點分別為
平行的切線,切點分別為![]() 、
、![]() ,小張馬上寫出了
,小張馬上寫出了![]() 、
、![]() 的面積,由此小張求出了直線
的面積,由此小張求出了直線![]() 與拋物線圍成的面積,你認為小張能做到嗎?請你說出理由.
與拋物線圍成的面積,你認為小張能做到嗎?請你說出理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校藝術專業300名學生參加某次測評,根據男女學生人數比例,使用分層抽樣的方法從中隨機抽取了100名學生,記錄他們的分數,將數據分成7組:[20,30),[30,40),…,[80,90],并整理得到如下頻率分布直方圖:
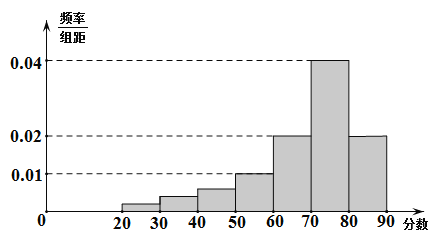
(1)從總體的300名學生中隨機抽取一人,估計其分數小于70的概率;
(2)已知樣本中分數小于40的學生有5人,試估計總體中分數在區間[40,50)內的人數;
(3)已知樣本中有一半男生的分數不小于70,且樣本中分數不小于70的男女生人數相等.試估計總體中男生和女生人數的比例.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線y2=2px的焦點為F,準線方程是x=﹣1.
(I)求此拋物線的方程;
(Ⅱ)設點M在此拋物線上,且|MF|=3,若O為坐標原點,求△OFM的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】閱讀下列有關光線的入射與反射的兩個事實現象:現象(1):光線經平面鏡反射滿足入射角與反射角相等(如圖);現象(2);光線從橢圓的一個焦點出發經橢圓反射后通過另一個焦點(如圖).試結合,上述事實現象完成下列問題:
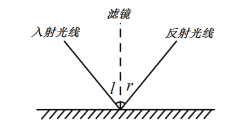
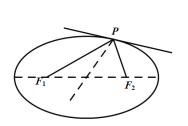
(Ⅰ)有一橢圓型臺球桌,長軸長為2a,短軸長為2b.將一放置于焦點處的桌球擊出.經過球桌邊緣的反射(假設球的反射充全符合現象(2)),后第一次返回到該焦點時所經過的路程記為S,求S的值(用a,b表示);
(Ⅱ)結論:橢圓![]() 上任點P(x0,y0)處的切線的方程為
上任點P(x0,y0)處的切線的方程為![]() .記橢圓C的方程為C:
.記橢圓C的方程為C:![]() ,在直線x=4上任一點M向橢圓C引切線,切點分別為A,B.求證:直線lAB恒過定點:
,在直線x=4上任一點M向橢圓C引切線,切點分別為A,B.求證:直線lAB恒過定點:
(Ⅲ)過點T(1,0)的直線l(直線l斜率不為0)與橢圓C:![]() 交于P、Q兩點,是否存在定點S(s,0),使得直線SP與SQ斜率之積為定值,若存在求出S坐標;若不存在,請說明理由.
交于P、Q兩點,是否存在定點S(s,0),使得直線SP與SQ斜率之積為定值,若存在求出S坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com