
【題目】如圖,在![]() 中,
中,![]() ,點P為
,點P為![]() 的中點,
的中點,![]() 交
交![]() 于點D,現將
于點D,現將![]() 沿
沿![]() 翻折至
翻折至![]() ,使得平面
,使得平面![]() 平面
平面![]() .
.
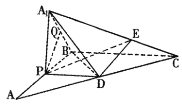
(1)若Q為線段![]() 的中點,求證:
的中點,求證:![]() 平面
平面![]() ;
;
(2)在線段![]() 上是否存在點E,使得二面角
上是否存在點E,使得二面角![]() 大小為
大小為![]() .若存在,請求出點E所在位置,若不存在,請說明理由.
.若存在,請求出點E所在位置,若不存在,請說明理由.
【答案】(1)證明見解析;(2)存在;E為線段![]() 的中點
的中點
【解析】
(1)推導出![]() ,
,![]() ,從而
,從而![]() ,推導出
,推導出![]() ,
,![]() ,進而
,進而![]() 平面
平面![]() ,由此能求出
,由此能求出![]() ,
,![]() ,由此能證明
,由此能證明![]() 平面
平面![]() .
.
(2)推導出![]() ,
,![]() ,得
,得![]() 平面
平面![]() ,以點
,以點![]() 為坐標原點,分別以
為坐標原點,分別以![]() ,
,![]() ,
,![]() 所在直線為
所在直線為![]() ,
,![]() ,
,![]() 軸,建立空間直角坐標系,當點
軸,建立空間直角坐標系,當點![]() 為線段
為線段![]() 的中點時,二面角
的中點時,二面角![]() 的大小為
的大小為![]() .
.
解:(1)證明:在![]() 中,
中,![]() ,
,![]() ,
,
![]() 將
將![]() 沿
沿![]() 翻折至
翻折至![]() ,
,![]() ,
,![]()
又![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
在![]() 中
中![]() ,Q為
,Q為![]() 的中點,
的中點,![]() ,
,
又![]() ,
,![]() 平面
平面![]()
(2)![]() 在
在![]() ,
,![]() ,
,![]() ,又
,又![]() 沿
沿![]() 翻折至
翻折至![]() ,
,
且平面![]() 平面
平面![]() ,由(1)有
,由(1)有![]() ,得
,得![]() 平面
平面![]() .
.
以點P為坐標原點,分別以![]() 所在直線為
所在直線為![]() 軸建立空間直角坐標系
軸建立空間直角坐標系![]() ,如圖所示.
,如圖所示.
則![]() ,
,
![]() .
.
設![]() ,則
,則![]() ,所以
,所以![]()
設平面![]() 的一個法向量為
的一個法向量為![]()
則由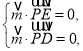 即
即![]()
可得![]()
可取平面![]() 的一個法向量為
的一個法向量為![]()
則 ,解得
,解得![]() .
.
所以當點E為線段![]() 的中點時,二面角
的中點時,二面角![]() 大小為
大小為![]() .
.


 開心練習課課練與單元檢測系列答案
開心練習課課練與單元檢測系列答案科目:高中數學 來源: 題型:
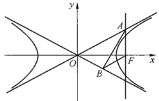
【題目】如圖,已知雙曲線![]() 的右焦點為F,點A,B分別在C的兩條漸近線上,
的右焦點為F,點A,B分別在C的兩條漸近線上,![]() 軸,
軸,![]() ,
,![]() (O為坐標原點).
(O為坐標原點).
(1)求雙曲線C的方程;
(2)過C上一點![]() 的直線
的直線![]() 與直線AF相交于點M,與直線
與直線AF相交于點M,與直線![]() 相交于點N.證明:當點P在C上移動時,
相交于點N.證明:當點P在C上移動時,![]() 恒為定值,并求此定值.
恒為定值,并求此定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2015全國高考試題)某公司為了解用戶對其產品的滿意度,從![]() ,
,![]() 兩地區分別隨機調查了20個用戶,得到用戶對產品的滿意度評分如下:
兩地區分別隨機調查了20個用戶,得到用戶對產品的滿意度評分如下:
![]() 地區:62 73 81 92 95 85 74 64 53 76
地區:62 73 81 92 95 85 74 64 53 76
78 86 95 66 97 78 88 82 76 89
![]() 地區:73 83 62 51 91 46 53 73 64 82
地區:73 83 62 51 91 46 53 73 64 82
93 48 65 81 74 56 54 76 65 79
根據用戶滿意度評分,將用戶的滿意度從低到高分為三個不同等級:
滿意度評分 | 低于70分 | 70分到89分 | 不低于90分 |
滿意度等級 | 不滿意 | 滿意 | 非常滿意 |
記事件![]() :“
:“![]() 地區用戶的滿意度等級高于
地區用戶的滿意度等級高于![]() 地區用戶的滿意度等級”假設兩地區用戶的評價結果相互獨立.根據所給數據,以事件發生的頻率作為相應事件發生的概率,求
地區用戶的滿意度等級”假設兩地區用戶的評價結果相互獨立.根據所給數據,以事件發生的頻率作為相應事件發生的概率,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是國家統計局于2020年1月9日發布的2018年12月到2019年12月全國居民消費價格的漲跌幅情況折線圖.(注:同比是指本期與同期作對比;環比是指本期與上期作對比.如:2019年2月與2018年2月相比較稱同比,2019年2月與2019年1月相比較稱環比)根據該折線圖,下列結論錯誤的是( )
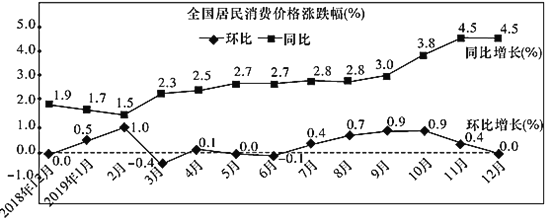
A.2019年12月份,全國居民消費價格環比持平
B.2018年12月至2019年12月全國居民消費價格環比均上漲
C.2018年12月至2019年12月全國居民消費價格同比均上漲
D.2018年11月的全國居民消費價格高于2017年12月的全國居民消費價格
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過雙曲線C:![]() 1(a>0,b>0)右焦點F2作雙曲線一條漸近線的垂線,垂足為P,與雙曲線交于點A,若
1(a>0,b>0)右焦點F2作雙曲線一條漸近線的垂線,垂足為P,與雙曲線交于點A,若![]() ,則雙曲線C的漸近線方程為( )
,則雙曲線C的漸近線方程為( )
A.y=±![]() xB.y=±xC.y=±2xD.y=±
xB.y=±xC.y=±2xD.y=±![]() x
x
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線C的參數方程為
中,曲線C的參數方程為![]() (
(![]() 為參數),以原點O為極點,x軸正半軸為極軸建立極坐標系,直線
為參數),以原點O為極點,x軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() ,且直線
,且直線![]() 與曲線C有兩個不同的交點.
與曲線C有兩個不同的交點.
(1)求實數a的取值范圍;
(2)已知M為曲線C上一點,且曲線C在點M處的切線與直線![]() 垂直,求點M的直角坐標.
垂直,求點M的直角坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某百貨商店今年春節期間舉行促銷活動,規定消費達到一定標準的顧客可進行一次抽獎活動,隨著抽獎活動的有效開展,參與抽獎活動的人數越來越多,該商店經理對春節前![]() 天參加抽獎活動的人數進行統計,
天參加抽獎活動的人數進行統計,![]() 表示第
表示第![]() 天參加抽獎活動的人數,得到統計表格如下:
天參加抽獎活動的人數,得到統計表格如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 5 | 8 | 8 | 10 | 14 | 15 | 17 |
(1)經過進一步統計分析,發現![]() 與
與![]() 具有線性相關關系.請根據上表提供的數據,用最小二乘法求出
具有線性相關關系.請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)該商店規定:若抽中“一等獎”,可領取600元購物券;抽中“二等獎”可領取300元購物券;抽中“謝謝惠顧”,則沒有購物券.已知一次抽獎活動獲得“一等獎”的概率為![]() ,獲得“二等獎”的概率為
,獲得“二等獎”的概率為![]() .現有張、王兩位先生參與了本次活動,且他們是否中獎相互獨立,求此二人所獲購物券總金額
.現有張、王兩位先生參與了本次活動,且他們是否中獎相互獨立,求此二人所獲購物券總金額![]() 的分布列及數學期望.
的分布列及數學期望.
參考公式: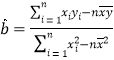 ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com