
【題目】已知函數![]() .
.
(1)求函數![]() 的單調區間;
的單調區間;
(2)是否存在一個正實數![]() ,滿足當
,滿足當![]() 時,
時,![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
【答案】(1)![]() 時,
時,![]() 的增函數區間為
的增函數區間為![]() ,無減函數區間;
,無減函數區間;![]() 時,
時,![]() 的增函數區間為
的增函數區間為![]() ,減函數區間為
,減函數區間為![]() ;
;![]() 時,
時,![]() 的增函數區間為
的增函數區間為![]() ,減函數區間為
,減函數區間為![]() ;(2)存在,
;(2)存在, ![]() .
.
【解析】
(1)根據題意,分析函數定義域,求導,分類討論參數不同的取值范圍時函數單調性,即可求解;
(2)根據題意,![]() ,由(1)知
,由(1)知![]() 的最大值為
的最大值為![]() ,若對任意實數
,若對任意實數![]() ,
,![]() 恒成立,只須使
恒成立,只須使![]() 即可.又因為
即可.又因為![]() ,所以不等式
,所以不等式![]() 等價于:
等價于:![]() ,即:
,即:![]() ,設
,設![]() ,對
,對![]() 求導,分析單調性,討論
求導,分析單調性,討論![]() 的范圍,判斷不等式成立條件.
的范圍,判斷不等式成立條件.
(1)函數![]() 的定義域為
的定義域為![]() ,
,
![]()
①若![]() 在
在![]() 上為增函數;
上為增函數;
②若![]() ,∵
,∵![]() ,∴當
,∴當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ;
;
所以![]() 在
在![]() 上為增函數,在
上為增函數,在![]() 上為減函數;
上為減函數;
③若![]() ,∵
,∵![]() ,∴當
,∴當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ;
;
所以![]() 在
在![]() 上為減函數,在
上為減函數,在![]() 為增函數
為增函數
綜上可知,![]() 時,
時,![]() 的增函數區間為
的增函數區間為![]() ,無減函數區間;
,無減函數區間;
![]() 時,
時,![]() 的增函數區間為
的增函數區間為![]() ,減函數區間為
,減函數區間為![]() ;
;
![]() 時,
時,![]() 的增函數區間為
的增函數區間為![]() ,減函數區間為
,減函數區間為![]() ;
;
(2)由(1)知,![]() 時,
時,![]() 的最大值為
的最大值為![]() ,
,
若對任意實數![]() ,
,![]() 恒成立,只須使
恒成立,只須使![]() 即可.
即可.
又因為![]() ,所以不等式
,所以不等式![]() 等價于:
等價于:![]() ,
,
即:![]() ,
,
設![]() ,則
,則![]() ,
,
∴當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]()
所以,![]() 在
在![]() 上為減函數,在
上為減函數,在![]() 上為增函數,
上為增函數,
∴當![]() 時,
時,![]() ,不等式
,不等式![]() 不成立,
不成立,
當![]() 時,
時,![]() ,不等式
,不等式![]() 不成立,
不成立,
當![]() 時,
時,![]() ,不等式
,不等式![]() 成立,
成立,
∴存在正實數![]() 且
且![]() 時,滿足當
時,滿足當![]() 時,
時,![]() 恒成立.
恒成立.


 快樂小博士鞏固與提高系列答案
快樂小博士鞏固與提高系列答案科目:高中數學 來源: 題型:
【題目】國家統計局服務業調查中心和中國物流與采購聯合會發布的2018年10月份至2019年9月份共12個月的中國制造業采購經理指數(PMI)如下圖所示.則下列結論中錯誤的是( )
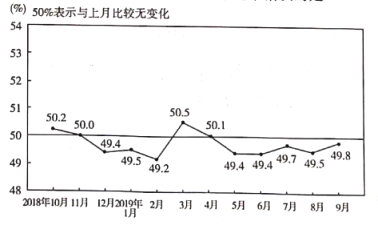
A.12個月的PMI值不低于50%的頻率為![]()
B.12個月的PMI值的平均值低于50%
C.12個月的PMI值的眾數為49.4%
D.12個月的PMI值的中位數為50.3%
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A.回歸直線![]() 至少經過其樣本數據
至少經過其樣本數據![]() 中的一個點
中的一個點
B.從獨立性檢驗可知有99%的把握認為吃地溝油與患胃腸癌有關系時,我們就說如果某人吃地溝油,那么他有99%可能患胃腸癌
C.在殘差圖中,殘差點分布的帶狀區域的寬度越狹窄,其模型擬合的精度越高
D.將一組數據的每一個數據都加上或減去同一個常數后,其方差也要加上或減去這個常數
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com