
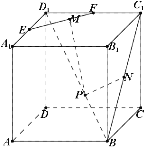
【題目】如圖,在棱長為![]() 的正方體
的正方體![]() 中,
中,![]() 分別為棱
分別為棱![]() 的中點,
的中點,![]() 是線段
是線段![]() 的中點,若點
的中點,若點![]() 分別為線段
分別為線段![]() 上的動點,則
上的動點,則![]() 的最小值為( )
的最小值為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
連接B1D1交EF于G,連接PG,則EF⊥平面B1D1DB,故EF⊥PG,從而PM的最小值PG,可知G為EF的中點,D1G為D1B1的四分之一.其次,連接BD,設其中點為H,連接PH,BC1,則△D1DB≌△D1C1B,從而PN=PH.(實現了轉化,這步是解題之關鍵),最后,連接GH交BD1于K,則當P為K時,PM+PN取得最小值,所求最小值為GH,即可得出結論.
首先PM的最小值就是P到EF的距離.
連接B1D1交EF于G,連接PG,則EF⊥平面B1D1DB,故EF⊥PG,從而PM的最小值PG,可知G為EF的中點,D1G為D1B1的四分之一.其次,連接BD,設其中點為H,連接PH,BC1,則△D1DB≌△D1C1B1,從而PN=PH.(實現了轉化,這步是解題之關鍵)
最后,連接GH交BD1于K,則當P為K時,PM+PN取得最小值,所求最小值為GH.
∵正方體ABCD﹣A1B1C1D1的棱長為1,
∴GH=![]() =
=![]() .
.
故選:D.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓E: ![]() =1(a>b>0)的離心率是
=1(a>b>0)的離心率是 ![]() ,過E的右焦點且垂直于橢圓長軸的直線與橢圓交于A,B兩點,|AB|=2.
,過E的右焦點且垂直于橢圓長軸的直線與橢圓交于A,B兩點,|AB|=2.
(Ⅰ)求橢圓方程;
(Ⅱ)過點P(0, ![]() )的動直線l與橢圓E交于的兩點M,N(不是的橢圓頂點),是否存在實數λ,使
)的動直線l與橢圓E交于的兩點M,N(不是的橢圓頂點),是否存在實數λ,使 ![]() +λ
+λ ![]() 為定值?若存在,求出λ的值;若不存在,請說明理由.
為定值?若存在,求出λ的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數g(x)滿足g(g(x))=n(n∈N)有n+3個解,則稱函數g(x)為“復合n+3解”函數.已知函數f(x)= 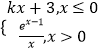 (其中e是自然對數的底數,e=2.71828…,k∈R),且函數f(x)為“復合5解”函數,則k的取值范圍是( )
(其中e是自然對數的底數,e=2.71828…,k∈R),且函數f(x)為“復合5解”函數,則k的取值范圍是( )
A.(﹣∞,0)
B.(﹣e,e)
C.(﹣1,1)
D.(0,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某校甲、乙、丙三個年級的學生志愿者人數分別為240,160,160.現采用分層抽樣的方法從中抽取7名同學去某敬老院參加獻愛心活動.
(Ⅰ)應從甲、乙、丙三個年級的學生志愿者中分別抽取多少人?
(Ⅱ)設抽出的7名同學分別用A,B,C,D,E,F,G表示,現從中隨機抽取2名同學承擔敬老院的衛生工作.
(i)試用所給字母列舉出所有可能的抽取結果;
(ii)設M為事件“抽取的2名同學來自同一年級”,求事件M發生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
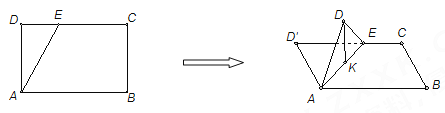
【題目】如圖,在長方形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 為線段
為線段![]() 上一動點,現將
上一動點,現將![]() 沿
沿![]() 折起,使點
折起,使點![]() 在面
在面![]() 內的射影
內的射影![]() 在直線
在直線![]() 上,當點
上,當點![]() 從
從![]() 運動到
運動到![]() ,則點
,則點![]() 所形成軌跡的長度為( )
所形成軌跡的長度為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系xOy中,傾斜角為α(α≠ ![]() )的直線l的參數方程為
)的直線l的參數方程為 ![]() (t為參數).以坐標原點為極點,以x軸的正半軸為極軸,建立極坐標系,曲線C的極坐標方程是ρcos2θ﹣4sinθ=0.
(t為參數).以坐標原點為極點,以x軸的正半軸為極軸,建立極坐標系,曲線C的極坐標方程是ρcos2θ﹣4sinθ=0.
(I)寫出直線l的普通方程和曲線C的直角坐標方程;
(Ⅱ)已知點P(1,0).若點M的極坐標為(1, ![]() ),直線l經過點M且與曲線C相交于A,B兩點,設線段AB的中點為Q,求|PQ|的值.
),直線l經過點M且與曲線C相交于A,B兩點,設線段AB的中點為Q,求|PQ|的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓 ![]() 的右焦點為F,設直線l:x=5與x軸的交點為E,過點F且斜率為k的直線l1與橢圓交于A,B兩點,M為線段EF的中點.
的右焦點為F,設直線l:x=5與x軸的交點為E,過點F且斜率為k的直線l1與橢圓交于A,B兩點,M為線段EF的中點.
(I)若直線l1的傾斜角為 ![]() ,求△ABM的面積S的值;
,求△ABM的面積S的值;
(Ⅱ)過點B作直線BN⊥l于點N,證明:A,M,N三點共線.
查看答案和解析>>
科目:高中數學 來源: 題型:
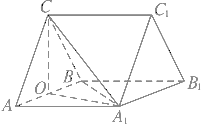
【題目】如圖,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
O為AB的中點
(1)證明:AB⊥平面A1OC
(2)若AB=CB=2,平面ABC![]() 平面A1ABB1,求三棱柱ABC-A1B1C1的體積.
平面A1ABB1,求三棱柱ABC-A1B1C1的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設樣本數據x1 , x2 , …,x2017的方差是4,若yi=2xi﹣1(i=1,2,…,2017),則y1 , y2 , …y2017的方差為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com