
【題目】已知函數![]() .
.
(Ⅰ)若函數![]() 在
在![]() 時取得極值,求實數
時取得極值,求實數![]() 的值;
的值;
(Ⅱ)當![]() 時,求
時,求![]() 零點的個數.
零點的個數.
【答案】(Ⅰ)1;(Ⅱ)兩個.
【解析】
(Ⅰ)![]() ,由
,由![]() ,解得
,解得![]() ,檢驗
,檢驗![]() 時取得極小值即可;(II)令
時取得極小值即可;(II)令![]() ,由
,由![]() ,得
,得![]() ,討論單調性得
,討論單調性得![]() 在
在![]() 時取得極小值,并證明極小值為
時取得極小值,并證明極小值為![]() .再由零點存在定理說明函數
.再由零點存在定理說明函數![]() 在
在![]() 和
和![]() 上各有一個零點,即可解得
上各有一個零點,即可解得
(I)![]() 定義域為
定義域為![]() .
.
![]() .
.
由已知,得![]() ,解得
,解得![]() .
.
當![]() 時,
時,![]() .
.
所以![]() .
.
所以![]() 減區間為
減區間為![]() ,增區間為
,增區間為![]() .
.
所以函數![]() 在
在![]() 時取得極小值,其極小值為
時取得極小值,其極小值為![]() ,符合題意
,符合題意
所以![]() .
.
(II)令![]() ,由
,由![]() ,得
,得![]() .
.
所以![]() .
.
所以![]() 減區間為
減區間為![]() ,增區間為
,增區間為![]() .
.
所以函數![]() 在
在![]() 時取得極小值,其極小值為
時取得極小值,其極小值為![]() .
.
因為![]() ,所以
,所以![]() .
.
所以![]() .所以
.所以![]() .
.
因為![]() ,
,
又因為![]() ,所以
,所以![]() .
.
所以![]() .
.
根據零點存在定理,函數![]() 在
在![]() 上有且僅有一個零點.
上有且僅有一個零點.
因為![]() ,
,![]() .
.
令![]() ,得
,得![]() .
.
又因為![]() ,所以
,所以![]() .
.
所以當![]() 時,
時,![]() .
.
根據零點存在定理,函數![]() 在
在![]() 上有且僅有一個零點.
上有且僅有一個零點.
所以,當![]() 時,
時,![]() 有兩個零點.
有兩個零點.


科目:高中數學 來源: 題型:
【題目】如圖1,在△![]() 中,
中,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點,
的中點,![]() 為
為![]() 的中點,
的中點,![]() ,
,![]() .將△
.將△![]() 沿
沿![]() 折起到△
折起到△![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,如圖2.
,如圖2.
(Ⅰ)求證:![]() ;
;
(Ⅱ)求直線![]() 和平面
和平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)線段![]() 上是否存在點
上是否存在點![]() ,使得直線
,使得直線![]() 和
和![]() 所成角的余弦值為
所成角的余弦值為![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.

圖1 圖2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,為了保護環境,實現城市綠化,某房地產公司要在拆遷地長方形ABCD處規劃一塊長方形地面HPGC,建造住宅小區公園,但不能越過文物保護區三角形AEF的邊線EF.已知AB=CD=200 m,BC=AD=160 m,AF=40 m,AE=60 m,問如何設計才能使公園占地面積最大,求出最大面積.
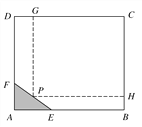
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題正確的個數是( )
①命題已知![]() 或
或![]() ,
,![]() ,則
,則![]() 是
是![]() 的充分不必要條件;
的充分不必要條件;
②“函數![]() 的最小正周期為
的最小正周期為![]() ”是“
”是“![]() ”的必要不充分條件;
”的必要不充分條件;
③![]() 在
在![]() 上恒成立
上恒成立![]() 在
在![]() 上恒成立;
上恒成立;
④“平面向量![]() 與
與![]() 的夾角是鈍角”的充要條件是“
的夾角是鈍角”的充要條件是“![]() ”
”
⑤命題![]() 函數
函數![]() 的值域為
的值域為![]() ,命題
,命題![]() 函數
函數![]() 是減函數.若
是減函數.若![]() 或
或![]() 為真命題,
為真命題,![]() 且
且![]() 為假命題,則實數
為假命題,則實數![]() 的取值范圍是
的取值范圍是![]() .
.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2sin2(x+![]() )-2
)-2![]() cos(x-
cos(x-![]() )-5a+2.
)-5a+2.
(1)設t=sinx+cosx,將函數f(x)表示為關于t的函數g(t),求g(t)的解析式;
(2)對任意x∈[0,![]() ],不等式f(x)≥6-2a恒成立,求a的取值范圍.
],不等式f(x)≥6-2a恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義域為R的函數f(x)=![]() 是奇函數.
是奇函數.
(1)求a,b的值;
(2)若對任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P-ABCD的底面是平行四邊形,PD⊥AB,O是AD的中點,BO=CO.
(1)求證:AB⊥平面PAD;
(2)若AD=2AB=4, PA=PD,點M在側棱PD上,且PD=3MD,二面角P-BC-D的大小為![]() ,求直線BP與平面MAC所成角的正弦值.
,求直線BP與平面MAC所成角的正弦值.
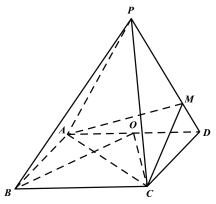
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com