（1）已知f(x)＝sinx＋2sin(
＋
)cos(＋)．(1)若f(α)＝
，α∈(－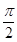
，0)，求α的值；
（2）若sin＝
，x∈(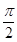，π)，求f(x)的值．
(1)
;(2)
.
【解析】
試題分析：(1)首先根據三角函數公式對函數
進行化簡,即
,從而
,則
,再由
,又
,從而求出
的值.(2)由
,則
,根據同角平方關系,由
,得
,再由倍角公式,可得
,
,從而求出函數的值.
試題解析：(1)f(x)＝sin x＋2sin(
＋
)cos(＋)
＝sin x＋sin(x＋
)＝sin x＋cos x＝
sin(x＋)，
由f(α)＝
，得sin(α＋)＝.
∴sin(α＋)＝
.
∵α∈(－，0)，∴α＋∈(－，)．
∴α＋＝
.∴α＝－
.
(2)∵x∈(，π)，∴∈(，)．
又sin＝
，∴cos＝
.
∴sin x＝2sincos＝
，
cos x＝－
＝－
.
∴f(x)＝sin x＋cos x＝－＝.
考點：三角函數的公式及化簡求值.
科目：高中數學 來源：四川省成都外國語學校2011－2012學年高一上學期期中考試數學試題 題型：022
給出下列四個命題，正確的命題是________；
①定義在R上的函數f(x)，函數y＝f(x－1)與y＝f(1－x)的圖象關于Y軸對稱；
②若f(x)＝gx－(k＋1)3x＋1＞0恒成立，則k的范圍是(－∞，1)；
③已知f(x)＝1＋log2x(1≤x≤16)，則函數y＝f2(x)＋f(x2)的值域是[2，34]；
④[x]表示不超過x的最大整數，當x是整數時[x]就是x，這個函數y＝[x]叫做“取整函數”．那么[log21]＋[log22]＋[log23]＋[log24]＋…＋[log2128]＝649．
查看答案和解析>>
科目：高中數學 來源： 題型：
已知f (x)＝
sin2x-cos2-
,I(x∈R).
(Ⅰ)求函數f (x)的最小值和最小正周期；
(Ⅱ)設
ABC的內角A、B、C的對邊分別為a、b、c，且c＝
，f (C)=0，若向量m＝(1,sinA)與向量n＝(2,sinB)共線，求a，b的值.
查看答案和解析>>
科目：高中數學 來源：2010-2011年江西省德興一中高二下學期第一次月考數學文卷 題型：解答題
（本小題滿分14分）
已知f(x)＝x2＋bx＋c為偶函數，曲線y＝f(x)過點(2,5)，g(x)＝(x＋a)f(x)．
(1)求f(x)的解析式；
(2)若曲線y＝g(x)有斜率為0的切線，求實數a的取值范圍；
(3)若當x＝1時，函數y＝g(x)取得極值，確定y＝g(x)的單調區間．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
是(－∞，＋∞)上的減函數，那么a的取值范圍是( )
)
，