
【題目】
如圖,長方體ABCD–A1B1C1D1的底面ABCD是正方形,點E在棱AA1上,BE⊥EC1.
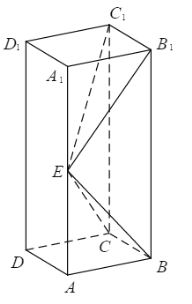
(1)證明:BE⊥平面EB1C1;
(2)若AE=A1E,求二面角B–EC–C1的正弦值.
【答案】(1)證明見解析;(2)![]()
【解析】
(1)利用長方體的性質,可以知道![]() 側面
側面![]() ,利用線面垂直的性質可以證明出
,利用線面垂直的性質可以證明出![]() ,這樣可以利用線面垂直的判定定理,證明出
,這樣可以利用線面垂直的判定定理,證明出![]() 平面
平面![]() ;
;
(2)以點![]() 坐標原點,以
坐標原點,以![]() 分別為
分別為![]() 軸,建立空間直角坐標系,
軸,建立空間直角坐標系,
設正方形![]() 的邊長為
的邊長為![]() ,
,![]() ,求出相應點的坐標,利用
,求出相應點的坐標,利用![]() ,可以求出
,可以求出![]() 之間的關系,分別求出平面
之間的關系,分別求出平面![]() 、平面
、平面![]() 的法向量,利用空間向量的數量積公式求出二面角
的法向量,利用空間向量的數量積公式求出二面角![]() 的余弦值的絕對值,最后利用同角的三角函數關系,求出二面角
的余弦值的絕對值,最后利用同角的三角函數關系,求出二面角![]() 的正弦值.
的正弦值.
證明(1)因為![]() 是長方體,所以
是長方體,所以![]() 側面
側面![]() ,而
,而![]() 平面
平面![]() ,所以
,所以![]()
又![]() ,
,![]() ,
,![]() 平面
平面![]() ,因此
,因此![]() 平面
平面![]() ;
;
(2)以點![]() 坐標原點,以
坐標原點,以![]() 分別為
分別為![]() 軸,建立如下圖所示的空間直角坐標系,
軸,建立如下圖所示的空間直角坐標系,
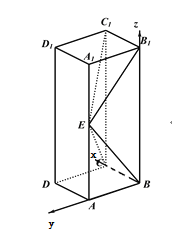
![]() ,
,
因為![]() ,所以
,所以![]() ,
,
所以![]() ,
,![]() ,
,
設![]() 是平面
是平面![]() 的法向量,
的法向量,
所以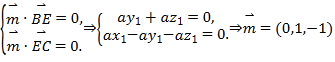 ,
,
設![]() 是平面
是平面![]() 的法向量,
的法向量,
所以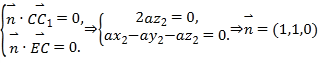 ,
,
二面角![]() 的余弦值的絕對值為
的余弦值的絕對值為 ,
,
所以二面角![]() 的正弦值為
的正弦值為![]() .
.


 輕松課堂單元期中期末專題沖刺100分系列答案
輕松課堂單元期中期末專題沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】如圖,AB是圓O的直徑,點C是圓O上異于A,B的點,PO垂直于圓O所在的平面,且![]() .D為線段AC的中點.
.D為線段AC的中點.
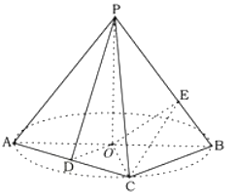
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若點E在線段PB上,且![]() ,求三棱錐
,求三棱錐![]() 體積的最大值.
體積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() ,其中
,其中![]() .點
.點![]() 在
在![]() 的焦點
的焦點![]() 的右側,且
的右側,且![]() 到
到![]() 的準線的距離是
的準線的距離是![]() 與
與![]() 距離的3倍.經過點
距離的3倍.經過點![]() 的直線與拋物線
的直線與拋物線![]() 交于不同的
交于不同的![]() 兩點,直線
兩點,直線![]() 與直線
與直線![]() 交于點
交于點![]() ,經過點
,經過點![]() 且與直線
且與直線![]() 垂直的直線
垂直的直線![]() 交
交![]() 軸于點
軸于點![]() .
.
(1)求拋物線的方程和![]() 的坐標;
的坐標;
(2)判斷直線![]() 與直線
與直線![]() 的位置關系,并說明理由.
的位置關系,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 是空氣質量的一個重要指標,我國
是空氣質量的一個重要指標,我國![]() 標準采用世衛組織設定的最寬限值,即
標準采用世衛組織設定的最寬限值,即![]() 日均值在
日均值在![]() 以下空氣質量為一級,在
以下空氣質量為一級,在![]() 之間空氣質量為二級,在
之間空氣質量為二級,在![]() 以上空氣質量為超標.如圖是某地
以上空氣質量為超標.如圖是某地![]() 月
月![]() 日到
日到![]() 日
日![]() 日均值(單位:
日均值(單位:![]() )的統計數據,則下列敘述不正確的是( )
)的統計數據,則下列敘述不正確的是( )
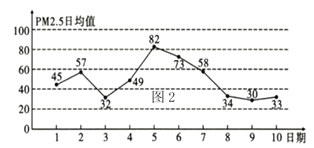
A.從![]() 日到
日到![]() 日,
日,![]() 日均值逐漸降低
日均值逐漸降低
B.這![]() 天的
天的![]() 日均值的中位數是
日均值的中位數是![]()
C.這![]() 天中
天中![]() 日均值的平均數是
日均值的平均數是![]()
D.從這![]() 天的日均
天的日均![]() 監測數據中隨機抽出一天的數據,空氣質量為一級的概率是
監測數據中隨機抽出一天的數據,空氣質量為一級的概率是![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 年
年![]() 月,電影《毒液》在中國上映,為了了解江西觀眾的滿意度,某影院隨機調查了本市觀看影片的觀眾,現從調查人群中隨機抽取部分觀眾.并用如圖所示的表格記錄了他們的滿意度分數(
月,電影《毒液》在中國上映,為了了解江西觀眾的滿意度,某影院隨機調查了本市觀看影片的觀眾,現從調查人群中隨機抽取部分觀眾.并用如圖所示的表格記錄了他們的滿意度分數(![]() 分制),若分數不低于
分制),若分數不低于![]() 分,則稱該觀眾為“滿意觀眾”,請根據下面尚未完成并有局部污損的頻率分布表(如圖所示),解決下列問題.
分,則稱該觀眾為“滿意觀眾”,請根據下面尚未完成并有局部污損的頻率分布表(如圖所示),解決下列問題.
組別 | 分組 | 頻數 | 頻率 |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
合計 |
|
|
(1)寫出![]() 、
、![]() 的值;
的值;
(2)畫出頻率分布直方圖,估算中位數;
(3)在選取的樣本中,從滿意觀眾中隨機抽取![]() 名觀眾領取獎品,求所抽取的
名觀眾領取獎品,求所抽取的![]() 名觀眾中至少有
名觀眾中至少有![]() 名觀眾來自第
名觀眾來自第![]() 組的概率.
組的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com