【題目】交強險是車主必須為機動車購買的險種，若普通6座以下私家車投保交強險第一年的費用 (基準保費)統一為
元，在下一年續保時，實行的是費率浮動機制，保費是與上一年度車輛發生道路交通安全違法行為或者道路交通事故的情況相聯系的.交強險第二年價格計算公式具體如下:交強險最終保費
基準保費
（
浮動比率
).發生交通事故的次數越多，出險次數的就越多，費率也就越髙，具體浮動情況如下表：
某機構為了研究某一品牌普通6座以下私家車的投保情況，為此搜集并整理了100輛這一品牌普通6座以下私家車一年內的出險次數，得到下面的柱狀圖：
已知小明家里有一輛該品牌普通6座以下私家車且需要續保，續保費用為
元.
（1）記
為事件“
”，求
的估計值；
（2）求
的平均估計值.
科目：高中數學 來源： 題型：
【題目】為響應市政府“綠色出行”的號召，王老師每個工作日上下班由自駕車改為選擇乘坐地鐵或騎共享單車這兩種方式中的一種出行．根據王老師從2017年3月到2017年5月的出行情況統計可知，王老師每次出行乘坐地鐵的概率是0.4，騎共享單車的概率是0.6．乘坐地鐵單程所需的費用是3元，騎共享單車單程所需的費用是1元．記王老師在一個工作日內上下班所花費的總交通費用為X元，假設王老師上下班選擇出行方式是相互獨立的．
（I）求X的分布列和數學期望 
；
（II）已知王老師在2017年6月的所有工作日（按22個工作日計）中共花費交通費用110元，請判斷王老師6月份的出行規律是否發生明顯變化，并依據以下原則說明理由．
原則：設 
表示王老師某月每個工作日出行的平均費用，若 
，則有95％的把握認為王老師該月的出行規律與前幾個月的出行規律相比有明顯變化．（注： 
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】等差數列{an}的前n項和為Sn ， 數列{bn}是等比數列，滿足a1=3，b1=1，b2+S2=10，a5﹣2b2=a3 ．
（Ⅰ）求數列{an}和{bn}的通項公式；
（Ⅱ）令Cn=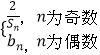 
設數列{cn}的前n項和Tn ， 求T2n ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】口袋中裝有2個白球和n（n≥2，n 
N*）個紅球．每次從袋中摸出2個球（每次摸球后把這2個球放回口袋中），若摸出的2個球顏色相同則為中獎，否則為不中獎．
（I）用含n的代數式表示1次摸球中獎的概率；
（Ⅱ）若n=3，求3次摸球中恰有1次中獎的概率；
（III）記3次摸球中恰有1次中獎的概率為f（p），當f（p）取得最大值時，求n的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知二次函數
的最小值為3，且
.
求函數
的解析式；
（2）若偶函數
（其中
），那么， 
在區間
上是否存在零點？請說明理由.
【答案】（1）
（2）存在零點
【解析】試題分析：（1）待定系數法，己知函數類型為二次函數，又知f(-1)=f(3),所以對稱軸是x=1,且函數最小值f(1)=3,所設函數
，且
，代入f(-1)=11，可解a。
（2）由題意可得
，代入
，由
和根的存在性定理， 
在區間（1，2）上存在零點。
試題解析：（1）因為
是二次函數，且
所以二次函數圖像的對稱軸為
．
又
的最小值為3，所以可設
，且
由
，得
所以
（2）由（1）可得
，
因為
，
所以
在區間（1，2）上存在零點．
【點睛】
（1）對于求己知類型函數的的解析式，常用待定系數法，由于二次函數的表達式形式比較多，有一般式，兩點式，頂點式，由本題所給條件知道對稱軸與頂點坐標，所以設頂點式。
（2）對于判定函數在否存在零點問題，一般解決此類問題的三步曲是：①先通過觀察函數圖象再估算出根所在的區間；②根據方程根的存在性定理證明根是存在的；③最后根據函數的性質證明根是唯一的.本題給了區間，可直接用根的存在性定理。
【題型】解答題
【結束】
20
【題目】《中華人民共和國個人所得稅》規定，公民月工資、薪金所得不超過3500元的部分不納稅，超過3500元的部分為全月稅所得額，此項稅款按下表分段累計計算：
全月應納稅所得額 | 稅率 |
不超過1500元的部分 |
|
超過1500元至4500元的部分 |
|
超過4500元至9000元的部分 |
|
（1）已知張先生的月工資，薪金所得為10000元，問他當月應繳納多少個人所得稅？
（2）設王先生的月工資，薪金所得為
，當月應繳納個人所得稅為
元，寫出
與
的函數關系式；
（3）已知王先生一月份應繳納個人所得稅為303元，那么他當月的工資、薪金所得為多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】袋內裝有6個球，每個球上都記有從1到6的一個號碼，設號碼為n的球重
克，這些球等可能地從袋里取出（不受重量、號碼的影響）.
（1）如果任意取出1個球，求其重量大于號碼數的概率；
（2）如果不放回地任意取出2個球，求它們重量相等的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
