
【題目】第7屆世界軍人運動會于2019年10月18日至27日在湖北武漢舉行,賽期10天,共設置射擊、游泳、田徑、籃球等27個大項,329個小項.共有來自100多個國家的近萬名現役軍人同臺競技.前期為迎接軍運會順利召開,武漢市很多單位和部門都開展了豐富多彩的宣傳和教育活動,努力讓大家更多的了解軍運會的相關知識,并倡議大家做文明公民.武漢市體育局為了解廣大民眾對軍運會知識的知曉情況,在全市開展了網上問卷調查,民眾參與度極高,現從大批參與者中隨機抽取200名幸運參與者,他們得分(滿分100分)數據,統計結果如下:
組別 |
|
|
|
|
|
|
|
頻數 | 5 | 30 | 40 | 50 | 45 | 20 | 10 |
(1)若此次問卷調查得分整體服從正態分布,用樣本來估計總體,設![]() ,
,![]() 分別為這200人得分的平均值和標準差(同一組數據用該區間中點值作為代表),求
分別為這200人得分的平均值和標準差(同一組數據用該區間中點值作為代表),求![]() ,
,![]() 的值(
的值(![]() ,
,![]() 的值四舍五入取整數),并計算
的值四舍五入取整數),并計算![]() ;
;
(2)在(1)的條件下,為感謝大家參與這次活動,市體育局還對參加問卷調查的幸運市民制定如下獎勵方案:得分低于![]() 的可以獲得1次抽獎機會,得分不低于
的可以獲得1次抽獎機會,得分不低于![]() 的可獲得2次抽獎機會,在一次抽獎中,抽中價值為15元的紀念品A的概率為
的可獲得2次抽獎機會,在一次抽獎中,抽中價值為15元的紀念品A的概率為![]() ,抽中價值為30元的紀念品B的概率為
,抽中價值為30元的紀念品B的概率為![]() .現有市民張先生參加了此次問卷調查并成為幸運參與者,記Y為他參加活動獲得紀念品的總價值,求Y的分布列和數學期望,并估算此次紀念品所需要的總金額.
.現有市民張先生參加了此次問卷調查并成為幸運參與者,記Y為他參加活動獲得紀念品的總價值,求Y的分布列和數學期望,并估算此次紀念品所需要的總金額.
(參考數據:![]() ;
;![]() ;
;![]() .)
.)
 浙江名校名師金卷系列答案
浙江名校名師金卷系列答案科目:高中數學 來源: 題型:
【題目】新疆小南瓜以沙甜聞名全國,小田計劃從新疆運輸小南瓜去上海,隨機從某瓜農的瓜地里挑選了100個,其質量分別在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (單位:克)中,經統計得頻率分布直方圖如圖所示,將頻率視為概率.
(單位:克)中,經統計得頻率分布直方圖如圖所示,將頻率視為概率.
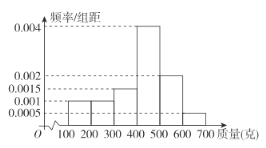
(1)請根據頻率分布直方圖估計該瓜農的小南瓜的平均質量;
(2)已知瓜地里還有2萬個小南瓜已經成熟,可以采摘,小田想全部購買,可是瓜農要求超過400克的小南瓜以5元一個的價格出售,其他的以3元一個的價格出售.將頻率視為概率,若新疆到上海往返的運費約2000元,請問這2萬個小南瓜在上海以每斤(500克)多少元定價才能保證小田的利潤不少于5000元?(結果保留一位小數)
(3)某天王阿姨在上海某超市的蔬菜柜臺上看到小田從新疆采摘的新疆小南瓜,已知柜臺上有若干個,若質量超過500克的小南瓜為“優質品”,王阿姨隨機購買了20個小南瓜,求王阿姨購買的小南瓜中“優質品”個數的期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,隨著我國汽車消費水平的提高,二手車流通行業得到迅猛發展.某汽車交易市場對2017年成交的二手車交易前的使用時間(以下簡稱“使用時間”)進行統計,得到頻率分布直方圖如圖1.


圖1 圖2
(1)記“在![]() 年成交的二手車中隨機選取一輛,該車的使用年限在
年成交的二手車中隨機選取一輛,該車的使用年限在![]() ”為事件
”為事件![]() ,試估計
,試估計![]() 的概率;
的概率;
(2)根據該汽車交易市場的歷史資料,得到散點圖如圖2,其中![]() (單位:年)表示二手車的使用時間,
(單位:年)表示二手車的使用時間,![]() (單位:萬元)表示相應的二手車的平均交易價格.由散點圖看出,可采用
(單位:萬元)表示相應的二手車的平均交易價格.由散點圖看出,可采用![]() 作為二手車平均交易價格
作為二手車平均交易價格![]() 關于其使用年限
關于其使用年限![]() 的回歸方程,相關數據如下表(表中
的回歸方程,相關數據如下表(表中![]() ,
,![]() ):
):

①根據回歸方程類型及表中數據,建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
②該汽車交易市場對使用8年以內(含8年)的二手車收取成交價格![]() 的傭金,對使用時間8年以上(不含8年)的二手車收取成交價格
的傭金,對使用時間8年以上(不含8年)的二手車收取成交價格![]() 的傭金.在圖1對使用時間的分組中,以各組的區間中點值代表該組的各個值.若以2017年的數據作為決策依據,計算該汽車交易市場對成交的每輛車收取的平均傭金.
的傭金.在圖1對使用時間的分組中,以各組的區間中點值代表該組的各個值.若以2017年的數據作為決策依據,計算該汽車交易市場對成交的每輛車收取的平均傭金.
附注:①對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為 ;
;
②參考數據:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知平面向量![]() ,
,![]() 滿足:|
滿足:|![]() |=2,|
|=2,|![]() |=1.
|=1.
(1)若(![]() 2
2![]() )(
)(![]() )=1,求
)=1,求![]()
![]() 的值;
的值;
(2)設向量![]() ,
,![]() 的夾角為θ.若存在t∈R,使得
的夾角為θ.若存在t∈R,使得![]() ,求cosθ的取值范圍.
,求cosθ的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“一帶一路”是“絲綢之路經濟帶”和“21世紀海上絲綢之路”的簡稱,旨在積極發展我國與沿線國家經濟合作關系,共同打造政治互信、經濟融合、文化包容的命運共同體.自2015年以來,“一帶一路”建設成果顯著.如圖是2015—2019年,我國對“一帶一路”沿線國家進出口情況統計圖,下列描述錯誤的是( )
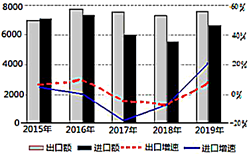
A.這五年,出口總額之和比進口總額之和大
B.這五年,2015年出口額最少
C.這五年,2019年進口增速最快
D.這五年,出口增速前四年逐年下降
查看答案和解析>>
科目:高中數學 來源: 題型:
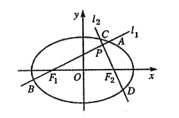
【題目】如圖,分別過橢圓![]() 左、右焦點
左、右焦點![]() 的動直線
的動直線![]() 相交于
相交于![]() 點,與橢圓
點,與橢圓![]() 分別交于
分別交于![]() 與
與![]() 不同四點,直線
不同四點,直線![]() 的斜率
的斜率![]() 滿足
滿足![]() .已知當
.已知當![]() 與
與![]() 軸重合時,
軸重合時,![]() ,
,![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)是否存在定點![]() ,使得
,使得![]() 為定值?若存在,求出
為定值?若存在,求出![]() 點坐標并求出此定值;若不存在,說明理由.
點坐標并求出此定值;若不存在,說明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ,
,![]() 和
和![]() .
.
【解析】試題分析:(1)當![]() 與
與![]() 軸重合時,
軸重合時,![]() 垂直于
垂直于![]() 軸,得
軸,得![]() ,得
,得![]() ,
,![]() 從而得橢圓的方程;(2)由題目分析如果存兩定點,則
從而得橢圓的方程;(2)由題目分析如果存兩定點,則![]() 點的軌跡是橢圓或者雙曲線 ,所以把
點的軌跡是橢圓或者雙曲線 ,所以把![]() 坐標化,可得
坐標化,可得![]() 點的軌跡是橢圓,從而求得定點
點的軌跡是橢圓,從而求得定點![]() 和點
和點![]() .
.
試題解析:![]() 當
當![]() 與
與![]() 軸重合時,
軸重合時,![]() , 即
, 即![]() ,所以
,所以![]() 垂直于
垂直于![]() 軸,得
軸,得![]() ,
,![]() ,, 得
,, 得![]() ,
,![]() 橢圓
橢圓![]() 的方程為
的方程為![]() .
.
![]() 焦點
焦點![]() 坐標分別為
坐標分別為![]() , 當直線
, 當直線![]() 或
或![]() 斜率不存在時,
斜率不存在時,![]() 點坐標為
點坐標為![]() 或
或![]() ;
;
當直線![]()
![]() 斜率存在時,設斜率分別為
斜率存在時,設斜率分別為![]() , 設
, 設![]()
![]() 由
由 , 得:
, 得:
![]() , 所以:
, 所以:![]() ,
,![]() , 則:
, 則:
![]()
![]() . 同理:
. 同理:![]()
![]() , 因為
, 因為
![]() , 所以
, 所以![]()
![]() , 即
, 即![]() , 由題意知
, 由題意知![]() , 所以
, 所以
![]() , 設
, 設![]() ,則
,則![]() ,即
,即![]() ,由當直線
,由當直線![]() 或
或![]() 斜率不存在時,
斜率不存在時,![]() 點坐標為
點坐標為![]() 或
或![]() 也滿足此方程,所以點
也滿足此方程,所以點![]() 在橢圓
在橢圓![]() 上.存在點
上.存在點![]() 和點
和點![]() ,使得
,使得![]() 為定值,定值為
為定值,定值為![]() .
.
考點:圓錐曲線的定義,性質,方程.
【方法點晴】本題是對圓錐曲線的綜合應用進行考查,第一問通過兩個特殊位置,得到基本量![]() ,
,![]() ,得
,得![]() ,
,![]() ,從而得橢圓的方程,第二問由題目分析如果存兩定點,則
,從而得橢圓的方程,第二問由題目分析如果存兩定點,則![]() 點的軌跡是橢圓或者雙曲線 ,本題的關鍵是從這個角度出發,把
點的軌跡是橢圓或者雙曲線 ,本題的關鍵是從這個角度出發,把![]() 坐標化,求得
坐標化,求得![]() 點的軌跡方程是橢圓
點的軌跡方程是橢圓![]() ,從而求得存在兩定點
,從而求得存在兩定點![]() 和點
和點![]() .
.
【題型】解答題
【結束】
21
【題目】已知![]() ,
,![]() ,
,![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的極值;
的極值;
(Ⅱ)若函數![]() 的兩個零點為
的兩個零點為![]() ,記
,記![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我區的中小學辦學條件在政府的教育督導下,迅速得到改變.督導一年后.分別隨機抽查了高中(用![]() 表示)與初中(用
表示)與初中(用![]() 表示)各10所學校.得到相關指標的綜合評價得分(百分制)的莖葉圖如圖所示.則從莖葉圖可得出正確的信息為(80分及以上為優秀)( )
表示)各10所學校.得到相關指標的綜合評價得分(百分制)的莖葉圖如圖所示.則從莖葉圖可得出正確的信息為(80分及以上為優秀)( )
①高中得分與初中得分的優秀率相同
②高中得分與初中得分的中位數相同
③高中得分的方差比初中得分的方差大
④高中得分與初中得分的平均分相同
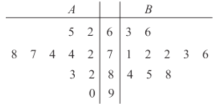
A.①②B.①③C.②④D.③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com