
【題目】如果數列![]() 對任意的
對任意的![]() 滿足:
滿足:![]() ,則稱數列
,則稱數列![]() 為“
為“![]() 數列”.
數列”.
(1)已知數列![]() 是“
是“![]() 數列”,設
數列”,設![]() ,求證:數列
,求證:數列![]() 是遞增數列,并指出
是遞增數列,并指出![]() 與
與![]() 的大小關系(不需要證明);
的大小關系(不需要證明);
(2)已知數列![]() 是首項為
是首項為![]() ,公差為
,公差為![]() 的等差數列,
的等差數列,![]() 是其前
是其前![]() 項的和,若數列
項的和,若數列![]() 是“
是“![]() 數列”,求
數列”,求![]() 的取值范圍;
的取值范圍;
(3)已知數列![]() 是各項均為正數的“
是各項均為正數的“![]() 數列”,對于
數列”,對于![]() 取相同的正整數時,比較
取相同的正整數時,比較![]() 和
和![]() 的大小,并說明理由.
的大小,并說明理由.
【答案】(1)![]() ;(2)
;(2)![]() (3)
(3)![]() ,證明見解析.
,證明見解析.
【解析】
(1)由新定義,結合單調性的定義可得數列![]() 是遞增數列;再根據
是遞增數列;再根據![]() ,
,![]() ,可得
,可得![]() ;
;
(2)運用新定義和等差數列的求和公式,解絕對值不等式即可得到所求范圍;
(3)對一切![]() ,有
,有![]() .運用數學歸納法證明,注意驗證
.運用數學歸納法證明,注意驗證![]() 成立;假設
成立;假設![]() 不等式成立,注意變形和運用新定義,即可得證.
不等式成立,注意變形和運用新定義,即可得證.
(1)證明:數列![]() 是“
是“![]() 數列”,可得
數列”,可得![]() ,
,
即![]() ,即
,即![]() ,
,
可得數列![]() 是遞增數列,
是遞增數列,
![]() .
.
(2)數列![]() 是“
是“![]() 數列”,
數列”,
可得![]() ,
,
即![]() ,
,
可得![]() ,
,
即有![]() ,或
,或 ,或
,或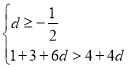 ,
,
即![]() 或
或![]() 或
或![]() ,
,
所以![]() .
.
(3)數列![]() 是各項均為正數的“
是各項均為正數的“![]() 數列”,
數列”,
對于![]() 取相同的正整數時,
取相同的正整數時,![]() ,
,
運用數學歸納法證明:
當![]() 時,
時,![]() ,
,![]() ,顯然
,顯然![]() 即
即![]() .
.
設![]() 時,
時,![]() .即
.即![]() ,
,
可得![]() ,
,
當![]() 時,即證
時,即證![]() ,
,
即證![]() ,
,
由![]()
![]() ,
,
即證
![]()
即證![]() ,
,
由![]() ,
,![]() ,
,![]() ,
,![]() ,
,
相加可得![]() ,
,
則對一切![]() ,有
,有![]() .
.


 導學教程高中新課標系列答案
導學教程高中新課標系列答案科目:高中數學 來源: 題型:
【題目】對于函數![]() ,
,![]() 且
且![]() 的定義域為
的定義域為![]() ,
,![]() .
.
(1)求實數![]() 的值,使函數
的值,使函數![]() 為奇函數;
為奇函數;
(2)在(1)的條件下,令![]() ,求使方程
,求使方程![]() ,
,![]() 有解的實數
有解的實數![]() 的取值范圍;
的取值范圍;
(3)在(1)的條件下,不等式![]() 對于任意的
對于任意的![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在R上的偶函數f(x),當x≥0時,f(x)=(x﹣1)2﹣1的圖象如圖所示,
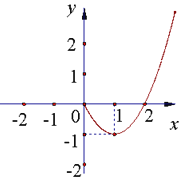
(1)請補全函數f(x)的圖象并寫出它的單調區間.
(2)根據圖形寫出函數f(x)的解析式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以平面直角坐標系的原點為極點,![]() 軸的正半軸為極軸,建立極坐標系,已知直線
軸的正半軸為極軸,建立極坐標系,已知直線![]() 的參數方程是
的參數方程是 (m>0,t為參數),曲線
(m>0,t為參數),曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與曲線
,與曲線![]() 交于點
交于點![]() ,且
,且![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,以坐標原點為極點, ![]() 軸的正半軸為極軸建立極坐標系,已知曲線
軸的正半軸為極軸建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,過點
,過點![]() 的直線
的直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),直線
為參數),直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點.
兩點.
(Ⅰ)寫出曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程;
的普通方程;
(Ⅱ)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在等腰梯形ABCD中,AB∥DC,AB=2,BC=1,∠ABC=60°.動點E和F分別在線段BC和DC上,且![]() .
.
(1)當λ![]() ,求|
,求|![]() |;
|;
(2)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為邊長為2的菱形,
為邊長為2的菱形,![]() ,
,![]() ,面
,面![]() 面
面![]() ,點
,點![]() 為棱
為棱![]() 的中點.
的中點.

(1)在棱![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 面
面![]() ,并說明理由;
,并說明理由;
(2)當二面角![]() 的余弦值為
的余弦值為![]() 時,求直線
時,求直線![]() 與平面
與平面![]() 所成的角.
所成的角.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某次的一次學科測試成績的莖葉圖和頻率分布直方圖都受到不同程度的污損,可見部分如圖.

(Ⅰ)求參加測試的總人數及分數在[80,90)之間的人數;
(Ⅱ)若要從分數在[80,100)之間的試卷中任取兩份分析學生失分情況,求在抽取的試卷中,恰有一份分數在[90,100)之間的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com