【題目】在等比數(shù)列{an}中，a1=2，a4=16
（1）求數(shù)列{an}的通項公式；
（2）令 
，n∈N* ， 求數(shù)列{bn}的前n項和Sn ．
【答案】
（1）解：設(shè)等比數(shù)列{an}的公比為q依題意a1=2，a4=16，得
∴q3=8，q=2，
∴an=2n
（2）解：由（1）得log2an=n，log2an+1=n+1，
bn= 
= 
﹣ 
∴Sn=b1+b2+…+bn=（1﹣ 
）+（ + 
）+…+（ ﹣ ）=1﹣ = 
【解析】（1）由“a1=2，a4=16”求得公比q再用通項公式求得通項．（2）先將 
= = ﹣ 轉(zhuǎn)化，再用裂項相消法求其前n項和Tn
【考點精析】認(rèn)真審題，首先需要了解等比數(shù)列的通項公式（及其變式）(通項公式：
)，還要掌握數(shù)列的前n項和(數(shù)列{an}的前n項和sn與通項an的關(guān)系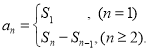
)的相關(guān)知識才是答題的關(guān)鍵．
世紀(jì)百通主體課堂小學(xué)課時同步達(dá)標(biāo)系列答案
世紀(jì)百通優(yōu)練測系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知等差數(shù)列{an}的首項為a，公差為b，且不等式ax2﹣3x+2＞0的解集為（﹣∞，1）∪（b，+∞）
（1）求數(shù)列{an}的通項公式
（2）設(shè)數(shù)列{bn}滿足= 
，求數(shù)列{bn}的前n項和Sn ．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)橢圓C： 
=1（a＞b＞0）過點（0，4），離心率為 
．
（1）求橢圓C的方程；
（2）求過點（3，0）且斜率為 
的直線被橢圓所截得線段的中點坐標(biāo)．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】10.已知{an}是正數(shù)組成的數(shù)列，a1=1，且點( 
，an+1)(n∈N*)在函數(shù)y=x2+1的圖象上.
（1）求數(shù)列{an}的通項公式.
（2）若數(shù)列{bn}滿足b1=1，bn+1=bn+ 
，求證：bn·bn+2< 
.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在銳角△ABC中，a，b，c分別為角A，B，C所對的邊，且 
a=2csinA．
（1）確定角C的大小；
（2）若c=3，且△ABC的面積為 
，求a2+b2的值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓
中心在坐標(biāo)原點,焦點在坐標(biāo)軸上,且經(jīng)過
三點.
(1)求橢圓
的方程;
(2)在直線
上任取一點
,連接
,分別與橢圓
交于
兩點,判斷直線
是否過定點?若是,求出該定點.若不是,請說明理由.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】(本題共12分）已知函數(shù)
(1)討論
的單調(diào)性；
(2)是否存在常數(shù)
，使
對任意的
和任意的
都成立，若存在，求出t的取值范圍；若不存在，請說明理由．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
