
【題目】已知函數![]() .
.
(1)解關于![]() 的不等式:
的不等式:![]() ;
;
(2)當![]() 時,過點
時,過點![]() 是否存在函數
是否存在函數![]() 圖象的切線?若存在,有多少條?若不存在,說明理由;
圖象的切線?若存在,有多少條?若不存在,說明理由;
(3)若![]() 是使
是使![]() 恒成立的最小值,試比較
恒成立的最小值,試比較![]() 與
與![]() 的大小(
的大小(![]() ).
).
【答案】(1)當![]() 時,
時,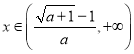 ;當
;當![]() 時,
時,![]() ;(2)不存在,理由見解析;(3)
;(2)不存在,理由見解析;(3)![]() .
.
【解析】
(1)當![]() 時,
時,![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() 時,
時,![]() ,解之即可;
,解之即可;
(2)由題意可得,切線斜率為![]() ,設
,設![]()
![]() ,求導可得
,求導可得![]() 在
在![]() 上遞減,
上遞減,![]() 上遞增,故
上遞增,故![]() ,所以方程無解,問題得解;
,所以方程無解,問題得解;
(3)由![]() 整理,得
整理,得![]() ,
,![]() 在
在![]() 上單調遞增,最小值1,所以
上單調遞增,最小值1,所以![]() ,即
,即![]() ,故
,故![]() ,
,![]() ,令
,令![]() ,可得
,可得![]() ,即可得出.
,即可得出.
(1)由已知![]() ,得
,得
當![]() 時,
時,![]() 的定義域為
的定義域為![]() ;當
;當![]() 時,
時,![]() 的定義域為
的定義域為![]()
①當![]() 時,
時,![]() ,原不等式等價于:
,原不等式等價于:
![]() ,
,
解得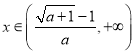 ;
;
②當![]() 時,
時,![]() ,原不等式等價于:
,原不等式等價于:
![]() ,
,
解得![]() .
.
(2)當![]() 時,
時,![]() ,
,
設![]() 上的切點坐標為
上的切點坐標為![]() ,顯然
,顯然![]() ,
,
求導,得![]() ,故切線斜率
,故切線斜率![]()
由題意,得![]() ,即
,即![]()
設![]() ,則
,則![]() ,
,
![]() 在
在![]() 上單調遞減;在
上單調遞減;在![]() 上單調遞增,
上單調遞增,
![]()
所以![]() 沒有實根,故不存在切線.
沒有實根,故不存在切線.
(3)由![]() 整理,得
整理,得![]()
由(2)可知,![]() 在
在![]() 上單調遞增,
上單調遞增,
所以當![]() 時
時![]() 取得最小值1,
取得最小值1,
由題意可得![]() ,即
,即![]() ,故
,故![]() ,
,
![]() .
.
令![]() ,則
,則![]() ,
,
而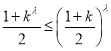 ,即
,即![]() ,
,
![]() ,
,
![]() .
.


科目:高中數學 來源: 題型:
【題目】已知項數為![]() 的數列
的數列![]() 滿足如下條件:①
滿足如下條件:①![]() ;②
;②![]() .若數列
.若數列![]() 滿足
滿足![]() ,其中
,其中![]() 則稱
則稱![]() 為
為![]() 的“心靈契合數列”.
的“心靈契合數列”.
(I)數列1,5,9,11,15是否存在“心靈契合數列”若存在,寫出其心靈契合數列,若不存在請說明理由;
(II)若![]() 為
為![]() 的“心靈契合數列”,判斷數列
的“心靈契合數列”,判斷數列![]() 的單調性,并予以證明;
的單調性,并予以證明;
(Ⅲ)已知數列![]() 存在“心靈契合數列”
存在“心靈契合數列”![]() ,且
,且![]() ,
,![]() ,求m的最大值.
,求m的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|2x﹣a|+|x﹣a+1|.
(1)當a=4時,求解不等式f(x)≥8;
(2)已知關于x的不等式f(x)![]() 在R上恒成立,求參數a的取值范圍.
在R上恒成立,求參數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】四川省雙流中學是一所國家級示范高中,具有悠久的辦學歷史、豐富的辦學經驗.近年來,雙中共為國內外高校輸送合格新生20000余名,其中為清華、北大、復旦、人大等一流學府輸送新生1800余名,上本科線人數年年超過千人,培養出省、市、縣高考冠軍17名,位居成都市同類學校前茅.該校高三某班有50名學生參加了今年成都市“一診”考試,其中英語成績服從正態分布![]() ,數學成績的頻率分布直方圖如下:
,數學成績的頻率分布直方圖如下:
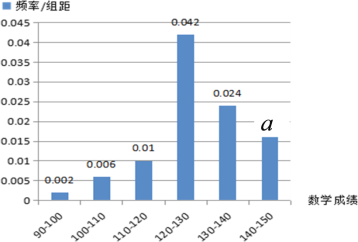
(1)如果成績140分及以上為單科特優,則該班本次考試中英語、數學單科特優大約各多少人?
(2)試問該班本次考試中英語和數學平均成績哪個較高,并說明理由;
(3)如果英語和數學兩科都為單科特優共有5人,把(1)中的近似數作為真實值,從(1)中這些同學中隨機抽取3人,設三人中英語和數學雙科特優的有![]() 人,求
人,求![]() 的分布列和數學期望.
的分布列和數學期望.
參考公式及數據:
![]() 則
則
![]()
![]()
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 與x軸負半軸交于
與x軸負半軸交于![]() ,離心率
,離心率![]() .
.
(1)求橢圓C的方程;
(2)設直線![]() 與橢圓C交于
與橢圓C交于![]() 兩點,連接AM,AN并延長交直線x=4于
兩點,連接AM,AN并延長交直線x=4于![]() 兩點,若
兩點,若![]() ,直線MN是否恒過定點,如果是,請求出定點坐標,如果不是,請說明理由.
,直線MN是否恒過定點,如果是,請求出定點坐標,如果不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
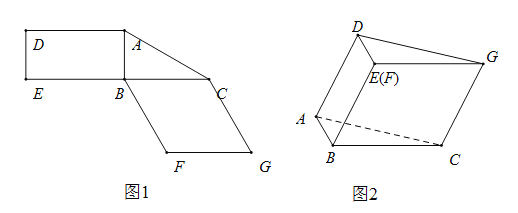
【題目】圖1是由矩形ADEB,Rt△ABC和菱形BFGC組成的一個平面圖形,其中AB=1,BE=BF=2,∠FBC=60°,將其沿AB,BC折起使得BE與BF重合,連結DG,如圖2.
(1)證明:圖2中的A,C,G,D四點共面,且平面ABC⊥平面BCGE;
(2)求圖2中的二面角BCGA的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(某工廠生產零件A,工人甲生產一件零件A,是一等品、二等品、三等品的概率分別為![]() ,工人乙生產一件零件A,是一等品、二等品、三等品的概率分別為
,工人乙生產一件零件A,是一等品、二等品、三等品的概率分別為![]() .己知生產一件一等品、二等品、三等品零件A給工廠帶來的效益分別為10元、5元、2元.
.己知生產一件一等品、二等品、三等品零件A給工廠帶來的效益分別為10元、5元、2元.
(1)試根據生產一件零件A給工廠帶來的效益的期望值判斷甲乙技術的好壞;
(2)為鼓勵工人提高技術,工廠進行技術大賽,最后甲乙兩人進入了決賽.決賽規則是:每一輪比賽,甲乙各生產一件零件A,如果一方生產的零件A品級優干另一方生產的零件,則該方得分1分,另一方得分-1分,如果兩人生產的零件A品級一樣,則兩方都不得分,當一方總分為4分時,比賽結束,該方獲勝.Pi+4(i=![]() 4,
4,![]() 3,
3,![]() 2,…,4)表示甲總分為i時,最終甲獲勝的概率.
2,…,4)表示甲總分為i時,最終甲獲勝的概率.
①寫出P0,P8的值;
②求決賽甲獲勝的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某貧困地區幾個丘陵的外圍有兩條相互垂直的直線型公路![]() ,以及鐵路線上的一條應開鑿的直線穿山隧道
,以及鐵路線上的一條應開鑿的直線穿山隧道![]() ,為進一步改善山區的交通現狀,計劃修建一條連接兩條公路
,為進一步改善山區的交通現狀,計劃修建一條連接兩條公路![]() 和山區邊界的直線型公路
和山區邊界的直線型公路![]() , 以
, 以![]() 所在的直線分別為
所在的直線分別為![]() 軸,
軸,![]() 軸, 建立平面直角坐標系
軸, 建立平面直角坐標系![]() , 如圖所示, 山區邊界曲線為
, 如圖所示, 山區邊界曲線為![]() ,設公路
,設公路![]() 與曲線
與曲線![]() 相切于點
相切于點![]() ,
,![]() 的橫坐標為
的橫坐標為![]() .
.
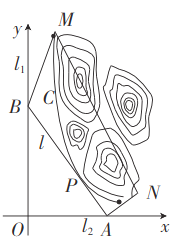
(1)當![]() 為何值時,公路
為何值時,公路![]() 的長度最短?求出最短長度;
的長度最短?求出最短長度;
(2)當公路![]() 的長度最短時,設公路
的長度最短時,設公路![]() 交
交![]() 軸,
軸,![]() 軸分別為
軸分別為![]() ,
,![]() 兩點,并測得四邊形
兩點,并測得四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() 千米,
千米,![]() 千米,求應開鑿的隧道
千米,求應開鑿的隧道![]() 的長度.
的長度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com