
【題目】已知三棱錐![]() (如圖一)的平面展開圖(如圖二)中,四邊形
(如圖一)的平面展開圖(如圖二)中,四邊形![]() 為邊長等于
為邊長等于![]() 的正方形,
的正方形,![]() 和
和![]() 均為正三角形,在三棱錐
均為正三角形,在三棱錐![]() 中:
中:
(I)證明:平面![]() 平面
平面![]() ;
;
(Ⅱ)若點![]() 在棱
在棱![]() 上運動,當直線
上運動,當直線![]() 與平面
與平面![]() 所成的角最大時,求二面角
所成的角最大時,求二面角![]() 的余弦值.
的余弦值.
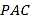
圖一
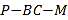
圖二
【答案】(1)見解析(2)![]()
【解析】
(1)設AC的中點為O,證明PO垂直AC,OB,結合平面與平面垂直判定,即可.(2)建立直角坐標系,分別計算兩相交平面的法向量,結合向量的數(shù)量積公式,計算夾角,即可.
(Ⅰ)設![]() 的中點為
的中點為![]() ,連接
,連接![]() ,
,![]() .
.
由題意,得![]() ,
,
![]() ,
,![]() .
.
因為在![]() 中,
中,![]() ,
,![]() 為
為![]() 的中點,
的中點,
所以![]() ,
,
因為在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,所以
,所以![]() .
.
因為![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
因為![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(Ⅱ)由(Ⅰ)知,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 是直線
是直線![]() 與平面
與平面![]() 所成的角,
所成的角,
且![]() ,
,
所以當![]() 最短時,即
最短時,即![]() 是
是![]() 的中點時,
的中點時,![]() 最大.
最大.
由![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,于是以
,于是以
![]() ,
,![]() ,
,![]() 所在直線分別為
所在直線分別為![]() 軸,
軸,![]() 軸,
軸,![]() 軸建立如圖示空間直角坐標系,
軸建立如圖示空間直角坐標系,
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
設平面![]() 的法向量為
的法向量為![]() ,則
,則
由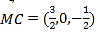 得:
得:![]() .
.
令![]() ,得
,得![]() ,
,![]() ,即
,即![]() .
.
設平面![]() 的法向量為
的法向量為![]() ,
,
由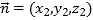 得:
得:![]() ,
,
令![]() ,得
,得![]() ,
,![]() ,即
,即![]() .
.
![]() .
.
由圖可知,二面角![]() 的余弦值為
的余弦值為![]() .
.


 高中必刷題系列答案
高中必刷題系列答案科目:高中數(shù)學 來源: 題型:
【題目】當前全世界人民越來越關注環(huán)境保護問題,某地某監(jiān)測站點于2018年8月起連續(xù)n天監(jiān)測空氣質(zhì)量指數(shù)(AQI),數(shù)據(jù)統(tǒng)計如下表:
空氣質(zhì)量指數(shù)(μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] |
空氣質(zhì)量等級 | 優(yōu) | 良 | 輕度污染 | 中度污染 | 重度污染 |
天數(shù) | 20 | 40 | m | 10 | 5 |
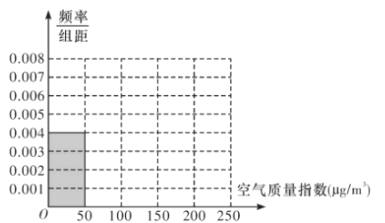
(1)根據(jù)所給統(tǒng)計表和頻率分布直方圖中的信息求出n,m的值,并完成頻率分布直方圖;
(2)由頻率分布直方圖,求該組數(shù)據(jù)的平均數(shù)與中位數(shù);
(3)在空氣質(zhì)量指數(shù)分別為[0,50]和(50,100]的監(jiān)測數(shù)據(jù)中,用分層抽樣的方法抽取6天,從中任意選取2天,求事件A“兩天空氣質(zhì)量等級都為良”發(fā)生的概率。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】隨著經(jīng)濟全球化、信息化的發(fā)展,企業(yè)之間的競爭從資源的爭奪轉向人才的競爭.吸引、留住培養(yǎng)和用好人才成為人力資源管理的戰(zhàn)略目標和緊迫任務.在此背景下,某信息網(wǎng)站在15個城市中對剛畢業(yè)的大學生的月平均收入薪資和月平均期望薪資做了調(diào)查,數(shù)據(jù)如圖所示.
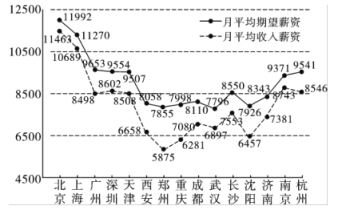
(1)若某大學畢業(yè)生從這15座城市中隨機選擇一座城市就業(yè),求該生選中月平均收人薪資高于8000元的城市的概率;
(2)若從月平均收入薪資與月平均期望薪資之差高于1000元的城市中隨機選擇2座城市,求這2座城市的月平均期望薪資都高于8000元或都低于8000元的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的四個頂點組成的四邊形的面積為
的四個頂點組成的四邊形的面積為![]() ,且經(jīng)過點
,且經(jīng)過點 .
.

(1)求橢圓![]() 的方程;
的方程;
(2)若橢圓![]() 的下頂點為
的下頂點為![]() ,如圖所示,點
,如圖所示,點![]() 為直線
為直線![]() 上的一個動點,過橢圓
上的一個動點,過橢圓![]() 的右焦點
的右焦點![]() 的直線
的直線![]() 垂直于
垂直于![]() ,且與
,且與![]() 交于
交于![]() 兩點,與
兩點,與![]() 交于點
交于點![]() ,四邊形
,四邊形![]() 和
和![]() 的面積分別為
的面積分別為![]() .求
.求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系xOy中,曲線C1的參數(shù)方程為![]() (
(![]() 為參數(shù))曲線C2的參數(shù)方程為
為參數(shù))曲線C2的參數(shù)方程為![]() (
(![]() ,
,![]() 為參數(shù))在以O為極點,x軸的正半軸為極軸的極坐標系中,射線l:θ=
為參數(shù))在以O為極點,x軸的正半軸為極軸的極坐標系中,射線l:θ=![]() 與C1,C2各有一個交點.當
與C1,C2各有一個交點.當![]() =0時,這兩個交點間的距離為2,當
=0時,這兩個交點間的距離為2,當![]() =
=![]() 時,這兩個交點重合.
時,這兩個交點重合.
(1)分別說明C1,C2是什么曲線,并求出a與b的值;
(2)設當![]() =
=![]() 時,l與C1,C2的交點分別為A1,B1,當
時,l與C1,C2的交點分別為A1,B1,當![]() =-
=-![]() 時,l與C1,C2的交點為A2,B2,求四邊形A1A2B2B1的面積.
時,l與C1,C2的交點為A2,B2,求四邊形A1A2B2B1的面積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標平面中,已知點![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,其中
,其中![]() 是正整數(shù),對平面上任一點
是正整數(shù),對平面上任一點![]() ,記
,記![]() 為
為![]() 關于點
關于點![]() 的對稱點,
的對稱點,![]() 為
為![]() 關于點
關于點![]() 的對稱點,…,
的對稱點,…,![]() 為
為![]() 關于點
關于點![]() 的對稱點.
的對稱點.
(1)求向量![]() 的坐標;
的坐標;
(2)當點![]() 在曲線
在曲線![]() 上移動時,點
上移動時,點![]() 的軌跡是函數(shù)
的軌跡是函數(shù)![]() 的圖像,其中
的圖像,其中![]() 是以3為周期的周期函數(shù),且當
是以3為周期的周期函數(shù),且當![]() 時,
時,![]() .求以曲線
.求以曲線![]() 為圖像的函數(shù)在
為圖像的函數(shù)在![]() 上的解析式;
上的解析式;
(3)對任意偶數(shù)![]() ,用
,用![]() 表示向量
表示向量![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,平面四邊形![]() 中,
中,![]() ,
,![]() 是
是![]() ,
,![]() 中點,
中點,![]() ,
,![]() ,
,![]() ,將
,將![]() 沿對角線
沿對角線![]() 折起至
折起至![]() ,使平面
,使平面![]() ,則四面體
,則四面體![]() 中,下列結論不正確的是( )
中,下列結論不正確的是( )
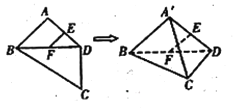
A.![]() 平面
平面![]()
B.異面直線![]() 與
與![]() 所成的角為
所成的角為![]()
C.異面直線![]() 與
與![]() 所成的角為
所成的角為![]()
D.直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 平面
平面![]() .底面
.底面![]() 是菱形,
是菱形,![]() .
.
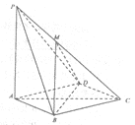
(Ⅰ)求證:直線![]() 平面
平面![]() ;
;
(Ⅱ)求直線![]() 與平面
與平面![]() 所成角的正切值;
所成角的正切值;
(Ⅲ)已知![]() 在線段
在線段![]() 上,且
上,且![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com