
【題目】我國古代名著《張丘建算經(jīng)》中記載:“今有方錐下廣二丈,高三丈,欲斬末為方亭;令上方六尺:問亭方幾何?”大致意思是:有一個(gè)四棱錐下底邊長為二丈,高三丈;現(xiàn)從上面截取一段,使之成為正四棱臺(tái)狀方亭,且四棱臺(tái)的上底邊長為六尺,則該正四棱臺(tái)的高為________尺,體積是_______立方尺(注:1丈=10尺).

| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】我市某區(qū)2018年房地產(chǎn)價(jià)格因“棚戶區(qū)改造”實(shí)行貨幣化補(bǔ)償,使房價(jià)快速走高,為抑制房價(jià)過快上漲,政府從2019年2月開始采用實(shí)物補(bǔ)償方式(以房換房),3月份開始房價(jià)得到很好的抑制,房價(jià)漸漸回落,以下是2019年2月后該區(qū)新建住宅銷售均價(jià)的數(shù)據(jù):
月份 | 3 | 4 | 5 | 6 | 7 |
價(jià)格 | 83 | 82 | 80 | 78 | 77 |
(1)研究發(fā)現(xiàn),3月至7月的各月均價(jià)![]() (百元/平方米)與月份
(百元/平方米)與月份![]() 之間具有較強(qiáng)的線性相關(guān)關(guān)系,求價(jià)格
之間具有較強(qiáng)的線性相關(guān)關(guān)系,求價(jià)格![]() (百元/平方米)關(guān)于月份
(百元/平方米)關(guān)于月份![]() 的線性回歸方程;
的線性回歸方程;
(2)用![]() 表示用(1)中所求的線性回歸方程得到的與
表示用(1)中所求的線性回歸方程得到的與![]() 對(duì)應(yīng)的銷售均價(jià)的估計(jì)值,3月份至7月份銷售均價(jià)估計(jì)值
對(duì)應(yīng)的銷售均價(jià)的估計(jì)值,3月份至7月份銷售均價(jià)估計(jì)值![]() 與實(shí)際相應(yīng)月份銷售均價(jià)
與實(shí)際相應(yīng)月份銷售均價(jià)![]() 差的絕對(duì)值記為
差的絕對(duì)值記為![]() ,即
,即![]() ,
,![]() .若
.若![]() ,則將銷售均價(jià)的數(shù)據(jù)
,則將銷售均價(jià)的數(shù)據(jù)![]() 稱為一個(gè)“好數(shù)據(jù)”,現(xiàn)從5個(gè)銷售均價(jià)數(shù)據(jù)中任取
稱為一個(gè)“好數(shù)據(jù)”,現(xiàn)從5個(gè)銷售均價(jià)數(shù)據(jù)中任取
參考公式:回歸方程系數(shù)公式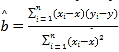 ,
,![]() ;參考數(shù)據(jù):
;參考數(shù)據(jù):![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為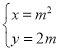 (
(![]() 為參數(shù)).以坐標(biāo)原點(diǎn)
為參數(shù)).以坐標(biāo)原點(diǎn)![]() 為極點(diǎn),
為極點(diǎn),![]() 軸正半軸為極軸建立極坐標(biāo)系,直線
軸正半軸為極軸建立極坐標(biāo)系,直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(Ⅰ)求直線![]() 的直角坐標(biāo)方程與曲線
的直角坐標(biāo)方程與曲線![]() 的普通方程;
的普通方程;
(Ⅱ)已知點(diǎn)![]() 設(shè)直線
設(shè)直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點(diǎn),求
兩點(diǎn),求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
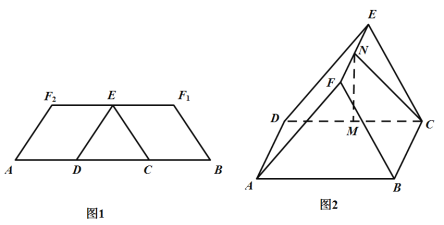
【題目】如圖1,在等腰梯形![]() 中,兩腰
中,兩腰![]() ,底邊
,底邊![]() 是
是![]() 的三等分點(diǎn),
的三等分點(diǎn),![]() 是
是![]() 的中點(diǎn).分別沿
的中點(diǎn).分別沿![]() 將四邊形
將四邊形![]() 和
和![]() 折起,使
折起,使![]() 重合于點(diǎn)
重合于點(diǎn)![]() ,得到如圖2所示的幾何體.在圖2中,
,得到如圖2所示的幾何體.在圖2中,![]() 分別為
分別為![]() 的中點(diǎn).
的中點(diǎn).
(1)證明:![]() 平面
平面![]()
(2)求幾何體![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),將曲線
為參數(shù)),將曲線![]() 上各點(diǎn)縱坐標(biāo)伸長到原來的2倍(橫坐標(biāo)不變)得到曲線
上各點(diǎn)縱坐標(biāo)伸長到原來的2倍(橫坐標(biāo)不變)得到曲線![]() ,以坐標(biāo)原點(diǎn)
,以坐標(biāo)原點(diǎn)![]() 為極點(diǎn),
為極點(diǎn),![]() 軸正半軸為極軸,建立極坐標(biāo)系,直線
軸正半軸為極軸,建立極坐標(biāo)系,直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)寫出![]() 的極坐標(biāo)方程與直線
的極坐標(biāo)方程與直線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)曲線![]() 上是否存在不同的兩點(diǎn)
上是否存在不同的兩點(diǎn)![]() ,
,![]() (以上兩點(diǎn)坐標(biāo)均為極坐標(biāo),
(以上兩點(diǎn)坐標(biāo)均為極坐標(biāo),![]() ,
,![]() ),使點(diǎn)
),使點(diǎn)![]() 、
、![]() 到
到![]() 的距離都為3?若存在,求
的距離都為3?若存在,求![]() 的值;若不存在,請(qǐng)說明理由.
的值;若不存在,請(qǐng)說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖1,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點(diǎn).現(xiàn)分別沿
的中點(diǎn).現(xiàn)分別沿![]() ,
,![]() 將
將![]() 和
和![]() 折起,點(diǎn)
折起,點(diǎn)![]() 折至點(diǎn)
折至點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 折至點(diǎn)
折至點(diǎn)![]() ,使得平面
,使得平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,連接
,連接![]() ,如圖2.
,如圖2.

(Ⅰ)若![]() 、
、![]() 分別為
分別為![]() 、
、![]() 的中點(diǎn),求證:平面
的中點(diǎn),求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)求多面體![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖1,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點(diǎn).現(xiàn)分別沿
的中點(diǎn).現(xiàn)分別沿![]() ,
,![]() 將
將![]() 和
和![]() 折起,點(diǎn)
折起,點(diǎn)![]() 折至點(diǎn)
折至點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 折至點(diǎn)
折至點(diǎn)![]() ,使得平面
,使得平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,連接
,連接![]() ,如圖2.
,如圖2.

(Ⅰ)若平面![]() 內(nèi)的動(dòng)點(diǎn)
內(nèi)的動(dòng)點(diǎn)![]() 滿足
滿足![]() 平面
平面![]() ,作出點(diǎn)
,作出點(diǎn)![]() 的軌跡并證明;
的軌跡并證明;
(Ⅱ)求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為推動(dòng)實(shí)施健康中國戰(zhàn)略,樹立國家大衛(wèi)生、大健康概念,手機(jī)APP也推出了多款健康運(yùn)動(dòng)軟件,如“微信運(yùn)動(dòng)”,楊老師的微信朋友圈內(nèi)有![]() 位好友參與了“微信運(yùn)動(dòng)”,他隨機(jī)選取了
位好友參與了“微信運(yùn)動(dòng)”,他隨機(jī)選取了![]() 位微信好友(女
位微信好友(女![]() 人,男
人,男![]() 人),統(tǒng)計(jì)其在某一天的走路步數(shù),其中,女性好友的走路步數(shù)數(shù)據(jù)記錄如下:
人),統(tǒng)計(jì)其在某一天的走路步數(shù),其中,女性好友的走路步數(shù)數(shù)據(jù)記錄如下:
5860 | 8520 | 7326 | 6798 | 7325 | 8430 | 3216 | 7453 | 11754 | 9860 |
8753 | 6450 | 7290 | 4850 | 10223 | 9763 | 7988 | 9176 | 6421 | 5980 |
男性好友走路的步數(shù)情況可分為五個(gè)類別:![]() 步(說明“
步(說明“![]() ”表示大于等于
”表示大于等于![]() ,小于等于
,小于等于![]() ,下同),
,下同),![]() 步,
步,![]() 步,
步,![]() 步及以上,且
步及以上,且![]() 三種類別人數(shù)比例為
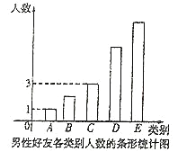
三種類別人數(shù)比例為![]() ,將統(tǒng)計(jì)結(jié)果繪制如圖所示的條形圖,若某人一天的走路步數(shù)超過
,將統(tǒng)計(jì)結(jié)果繪制如圖所示的條形圖,若某人一天的走路步數(shù)超過![]() 步被系統(tǒng)認(rèn)定為“衛(wèi)健型”,否則被系統(tǒng)認(rèn)定為“進(jìn)步型”.
步被系統(tǒng)認(rèn)定為“衛(wèi)健型”,否則被系統(tǒng)認(rèn)定為“進(jìn)步型”.
(1)若以楊老師選取的好友當(dāng)天行走步數(shù)的頻率分布來估計(jì)所有微信好友每日走路步數(shù)的概率分布,請(qǐng)估計(jì)楊老師的微信好友圈里參與“微信運(yùn)動(dòng)”的![]() 名好友中,每天走路步數(shù)在
名好友中,每天走路步數(shù)在![]() 步的人數(shù);
步的人數(shù);
(2)請(qǐng)根據(jù)選取的樣本數(shù)據(jù)完成下面的![]() 列聯(lián)表并據(jù)此判斷能否有
列聯(lián)表并據(jù)此判斷能否有![]() 以上的把握認(rèn)定“認(rèn)定類型”與“性別”有關(guān)?
以上的把握認(rèn)定“認(rèn)定類型”與“性別”有關(guān)?
衛(wèi)健型 | 進(jìn)步型 | 總計(jì) | |
男 | 20 | ||
女 | 20 | ||
總計(jì) | 40 |
附: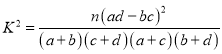 ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com