
【題目】設(shè)數(shù)列![]() 對(duì)任意
對(duì)任意![]() 都有
都有![]() (其中
(其中![]() 、
、![]() 、
、![]() 是常數(shù)) .
是常數(shù)) .
(Ⅰ)當(dāng)![]() ,
,![]() ,
,![]() 時(shí),求
時(shí),求![]() ;
;
(Ⅱ)當(dāng)![]() ,
,![]() ,
,![]() 時(shí),若
時(shí),若![]() ,
,![]() ,求數(shù)列
,求數(shù)列![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(Ⅲ)若數(shù)列![]() 中任意(不同)兩項(xiàng)之和仍是該數(shù)列中的一項(xiàng),則稱該數(shù)列是“封閉數(shù)列”.當(dāng)
中任意(不同)兩項(xiàng)之和仍是該數(shù)列中的一項(xiàng),則稱該數(shù)列是“封閉數(shù)列”.當(dāng)![]() ,
,![]() ,
,![]() 時(shí),設(shè)
時(shí),設(shè)![]() 是數(shù)列
是數(shù)列![]() 的前
的前![]() 項(xiàng)和,
項(xiàng)和,![]() ,試問:是否存在這樣的“封閉數(shù)列”,使得對(duì)任意
,試問:是否存在這樣的“封閉數(shù)列”,使得對(duì)任意![]() ,都有
,都有![]() ,且
,且![]() .若存在,求數(shù)列
.若存在,求數(shù)列![]() 的首項(xiàng)
的首項(xiàng)![]() 的所有取值;若不存在,說明理由.
的所有取值;若不存在,說明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅱ)存在,
;(Ⅱ)存在,![]()
【解析】
(Ⅰ)當(dāng)![]() ,
,![]() ,
,![]() 時(shí),由已知條件推導(dǎo)出
時(shí),由已知條件推導(dǎo)出![]() ,
,![]() ,由此得到數(shù)列
,由此得到數(shù)列![]() 是以首項(xiàng)為1,公比為3的等比數(shù)列,從而能求出
是以首項(xiàng)為1,公比為3的等比數(shù)列,從而能求出![]() ;
;
(Ⅱ)當(dāng)![]() ,
,![]() ,
,![]() ,由已知條件推導(dǎo)出
,由已知條件推導(dǎo)出![]() ,從而得到數(shù)列
,從而得到數(shù)列![]() 是等差數(shù)列,由此求出
是等差數(shù)列,由此求出![]() ;
;
(Ⅲ)由(Ⅱ)知數(shù)列![]() 是等差數(shù)列,
是等差數(shù)列,![]() ,由此進(jìn)行驗(yàn)證,求出數(shù)列
,由此進(jìn)行驗(yàn)證,求出數(shù)列![]() 的首項(xiàng)
的首項(xiàng)![]() 的所有取值.
的所有取值.
(Ⅰ)當(dāng)![]() ,
,![]() ,
,![]() 時(shí),
時(shí),![]()
![]() ①,用
①,用![]() 去換
去換
![]() 得
得![]()
![]() ②,②-①得,
②,②-①得,![]() ,即
,即![]() ,
,
在①中令![]() 得
得![]() ,故
,故![]() 是以1為首項(xiàng),3為公比的等比數(shù)列,所以
是以1為首項(xiàng),3為公比的等比數(shù)列,所以![]() ,
,
從而![]() .
.
(Ⅱ)當(dāng)![]() ,
,![]() ,
,![]() 時(shí),
時(shí),![]()
![]() ③,用
③,用![]() 去換
去換![]() 得
得
![]()
![]() ④,④-③得,
④,④-③得,![]() ⑤,用
⑤,用
![]() 去換
去換![]() 得
得![]() ⑥,⑥-⑤得,
⑥,⑥-⑤得,![]() ,即
,即
![]() ,故
,故![]() 是等差數(shù)列,因?yàn)?/span>
是等差數(shù)列,因?yàn)?/span>![]() ,
,![]() ,所以公差
,所以公差![]() ,
,
故![]() .
.
(Ⅲ)由(Ⅱ)知![]() 是等差數(shù)列,因
是等差數(shù)列,因![]() ,所以
,所以![]() ,假設(shè)存在這樣的“封閉數(shù)列”,
,假設(shè)存在這樣的“封閉數(shù)列”,
則對(duì)任意![]() ,必存在
,必存在![]() ,使得
,使得![]()
![]()
![]() ,
,
所以![]() ,故
,故![]() 為偶數(shù),
為偶數(shù),![]() ,又由已知,
,又由已知,![]() ,
,
所以![]() ,此時(shí)
,此時(shí)![]() ;當(dāng)
;當(dāng)![]() 時(shí),
時(shí),![]() ,
,
![]() ,所以
,所以![]()
![]() ,
,
故![]()


 互動(dòng)英語系列答案
互動(dòng)英語系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】春季氣溫逐漸攀升,病菌滋生傳播快,為了確保安全開學(xué),學(xué)校按30名學(xué)生一批,組織學(xué)生進(jìn)行某種傳染病毒的篩查,學(xué)生先到醫(yī)務(wù)室進(jìn)行血檢,檢呈陽性者需到防疫部門]做進(jìn)一步檢測(cè).學(xué)校綜合考慮了組織管理、醫(yī)學(xué)檢驗(yàn)?zāi)芰Φ榷嗳f面的因素,根據(jù)經(jīng)驗(yàn),采用分組檢測(cè)法可有效減少工作量,具體操作如下:將待檢學(xué)生隨機(jī)等分成若干組,先將每組的血樣混在一起化驗(yàn),若結(jié)果呈陰性,則可斷定本組血樣合格,不必再做進(jìn)一步的檢測(cè);若結(jié)果呈陽性,則本組中的每名學(xué)生再逐個(gè)進(jìn)行檢測(cè).現(xiàn)有兩個(gè)分組方案:方案一:將30人分成5組,每組6人;方案二:將30人分成6組,每組5人.已知隨機(jī)抽一人血檢呈陽性的概率為0.5%,且每個(gè)人血檢是否呈陽性相互獨(dú)立.
(Ⅰ)請(qǐng)幫學(xué)校計(jì)算一下哪一個(gè)分組方案的工作量較少?
(Ⅱ)已知該傳染疾病的患病率為0.45%,且患該傳染疾病者血檢呈陽性的概率為99.9%,若檢測(cè)中有一人血檢呈陽性,求其確實(shí)患該傳染疾病的概率.(參考數(shù)據(jù):(![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知點(diǎn)![]() 是拋物線
是拋物線![]() 的準(zhǔn)線上一點(diǎn),F為拋物線的焦點(diǎn),P為拋物線上的點(diǎn),且
的準(zhǔn)線上一點(diǎn),F為拋物線的焦點(diǎn),P為拋物線上的點(diǎn),且![]() ,若雙曲線C中心在原點(diǎn),F是它的一個(gè)焦點(diǎn),且過P點(diǎn),當(dāng)m取最小值時(shí),雙曲線C的離心率為______.
,若雙曲線C中心在原點(diǎn),F是它的一個(gè)焦點(diǎn),且過P點(diǎn),當(dāng)m取最小值時(shí),雙曲線C的離心率為______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某市組織高三全體學(xué)生參加計(jì)算機(jī)操作比賽,等級(jí)分為1至10分,隨機(jī)調(diào)閱了A、B兩所學(xué)校各60名學(xué)生的成績(jī),得到樣本數(shù)據(jù)如下:
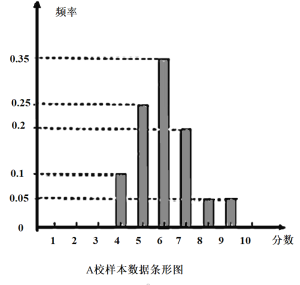
B校樣本數(shù)據(jù)統(tǒng)計(jì)表:
成績(jī)(分) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
人數(shù)(個(gè)) | 0 | 0 | 0 | 9 | 12 | 21 | 9 | 6 | 3 | 0 |
(1)計(jì)算兩校樣本數(shù)據(jù)的均值和方差,并根據(jù)所得數(shù)據(jù)進(jìn)行比較.
(2)從A校樣本數(shù)據(jù)成績(jī)分別為7分、8分和9分的學(xué)生中按分層抽樣方法抽取6人,若從抽取的6人中任選2人參加更高一級(jí)的比賽,求這2人成績(jī)之和大于或等于15的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() =0時(shí),求實(shí)數(shù)的m值及曲線
=0時(shí),求實(shí)數(shù)的m值及曲線![]() 在點(diǎn)(1,
在點(diǎn)(1, ![]() )處的切線方程;
)處的切線方程;
(2)討論函數(shù)![]() 的單調(diào)性.
的單調(diào)性.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=|x-m|-|2x+2m|(m>0).
(Ⅰ)當(dāng)m=1時(shí),求不等式f(x)≥1的解集;
(Ⅱ)若x∈R,t∈R,使得f(x)+|t-1|<|t+1|,求實(shí)數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓E:![]() (
(![]() )的離心率為
)的離心率為![]() ,F是E的右焦點(diǎn),過點(diǎn)F的直線交E于點(diǎn)
,F是E的右焦點(diǎn),過點(diǎn)F的直線交E于點(diǎn)![]() 和點(diǎn)
和點(diǎn)![]() (
(![]() ).當(dāng)直線
).當(dāng)直線![]() 與x軸垂直時(shí),
與x軸垂直時(shí),![]() .
.
(1)求橢圓E的方程;
(2)設(shè)直線l:![]() 交x軸于點(diǎn)G,過點(diǎn)B作x軸的平行線交直線l于點(diǎn)C.求證:直線
交x軸于點(diǎn)G,過點(diǎn)B作x軸的平行線交直線l于點(diǎn)C.求證:直線![]() 過線段
過線段![]() 的中點(diǎn).
的中點(diǎn).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某工廠![]() ,
,![]() 兩條相互獨(dú)立的生產(chǎn)線生產(chǎn)同款產(chǎn)品,在產(chǎn)量一樣的情況下,通過日常監(jiān)控得知,
兩條相互獨(dú)立的生產(chǎn)線生產(chǎn)同款產(chǎn)品,在產(chǎn)量一樣的情況下,通過日常監(jiān)控得知,![]() ,
,![]() 生產(chǎn)線生產(chǎn)的產(chǎn)品為合格品的概率分別為
生產(chǎn)線生產(chǎn)的產(chǎn)品為合格品的概率分別為![]() 和
和![]() .
.
(1)從![]() ,
,![]() 生產(chǎn)線上各抽檢一件產(chǎn)品,若使得產(chǎn)品至少有一件合格的概率不低于99.5%,求
生產(chǎn)線上各抽檢一件產(chǎn)品,若使得產(chǎn)品至少有一件合格的概率不低于99.5%,求![]() 的最小值
的最小值![]() ;
;
(2)假設(shè)不合格的產(chǎn)品均可進(jìn)行返工修復(fù)為合格品,以(1)中確定的![]() 作為
作為![]() 的值.
的值.
①已知![]() ,
,![]() 生產(chǎn)線的不合格品返工后每件產(chǎn)品可分別挽回?fù)p失5元和3元,若從兩條生產(chǎn)線上各隨機(jī)抽檢1000件產(chǎn)品,以挽回?fù)p失的平均數(shù)為判斷依據(jù),估計(jì)哪條生產(chǎn)線的挽回?fù)p失較多?
生產(chǎn)線的不合格品返工后每件產(chǎn)品可分別挽回?fù)p失5元和3元,若從兩條生產(chǎn)線上各隨機(jī)抽檢1000件產(chǎn)品,以挽回?fù)p失的平均數(shù)為判斷依據(jù),估計(jì)哪條生產(chǎn)線的挽回?fù)p失較多?
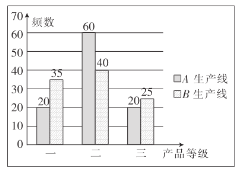
②若最終的合格品(包括返工修復(fù)后的合格品)按照一、二、三等級(jí)分類后,每件可分別獲利10元、8元、6元,現(xiàn)從![]() ,
,![]() 生產(chǎn)線的最終合格品中各隨機(jī)抽取100件進(jìn)行分級(jí)檢測(cè),結(jié)果統(tǒng)計(jì)如圖所示,用樣本的頻率分布估計(jì)總體分布,記該工廠生產(chǎn)一件產(chǎn)品的利潤(rùn)為
生產(chǎn)線的最終合格品中各隨機(jī)抽取100件進(jìn)行分級(jí)檢測(cè),結(jié)果統(tǒng)計(jì)如圖所示,用樣本的頻率分布估計(jì)總體分布,記該工廠生產(chǎn)一件產(chǎn)品的利潤(rùn)為![]() ,求
,求![]() 的分布列并估計(jì)該廠產(chǎn)量2000件時(shí)利潤(rùn)的期望值.
的分布列并估計(jì)該廠產(chǎn)量2000件時(shí)利潤(rùn)的期望值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com