
【題目】已知橢圓![]() 的長軸與短軸比值是2,橢圓C過點
的長軸與短軸比值是2,橢圓C過點![]() .
.
(1)求橢圓C的標(biāo)準(zhǔn)方程;
(2)過點![]() 作圓x2+y2=1的切線
作圓x2+y2=1的切線![]() 交橢圓C于A,B兩點,記△AOB(O為坐標(biāo)原點)的面積為S△AOB,將S△AOB表示為m的函數(shù),并求S△AOB的最大值
交橢圓C于A,B兩點,記△AOB(O為坐標(biāo)原點)的面積為S△AOB,將S△AOB表示為m的函數(shù),并求S△AOB的最大值
【答案】(1)![]() (2)
(2)![]() ,m∈(-∞,-1]∪[1,+∞);S△AOB的最大值為1
,m∈(-∞,-1]∪[1,+∞);S△AOB的最大值為1
【解析】
(1) 由已知可知![]() ,及橢圓C過點
,及橢圓C過點![]() ,代入橢圓方程即可求得
,代入橢圓方程即可求得![]() ,進而得出結(jié)果.
,進而得出結(jié)果.
(2) 由題設(shè)知切線![]() 的斜率存在,設(shè)切線
的斜率存在,設(shè)切線![]() 的方程為
的方程為![]() ,與橢圓方程聯(lián)立求得弦長
,與橢圓方程聯(lián)立求得弦長![]() ,由于
,由于![]() 與圓
與圓![]() 相切,可得
相切,可得![]() =1,化簡可得
=1,化簡可得![]() ,利用基本不等式化簡即可求得結(jié)果.
,利用基本不等式化簡即可求得結(jié)果.
解:(1)∵橢圓![]() 的長軸與短軸比值是2,
的長軸與短軸比值是2,
∴![]() ,設(shè)橢圓C的方程為:
,設(shè)橢圓C的方程為:![]() ,
,
∵橢圓C過點![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴橢圓C的標(biāo)準(zhǔn)方程為![]() .
.
(2)由題意知,![]() .
.
由題設(shè)知切線![]() 的斜率存在,設(shè)切線
的斜率存在,設(shè)切線![]() 的方程為
的方程為![]() ,
,
由 ,得
,得![]() ,
,
設(shè)A、B兩點的坐標(biāo)分別為(x1,y1)(x2,y2),
則![]() ,
,
又∵![]() 與圓
與圓![]() 相切,
相切,
∴![]() =1,
=1,![]() ,
,
∴![]() =
=![]()
=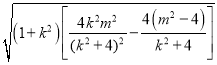
=![]() ,
,
∴![]() ,
,![]()
∴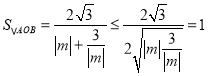 (當(dāng)且僅當(dāng)
(當(dāng)且僅當(dāng)![]() 時取等號)
時取等號)
∴當(dāng)![]() 時,S△AOB的最大值為1.
時,S△AOB的最大值為1.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】在菱形![]() 中,
中,![]() ,
,![]() 為線段
為線段![]() 的中點(如圖1).將
的中點(如圖1).將![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,
,![]() 為線段
為線段![]() 的中點(如圖2).
的中點(如圖2).
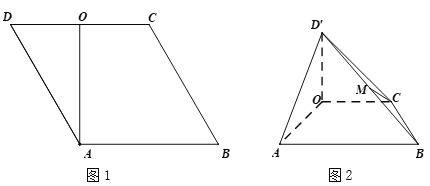
(Ⅰ)求證:![]() ;
;
(Ⅱ)求證:![]() 平面
平面![]() ;
;
(Ⅲ)當(dāng)四棱錐![]() 的體積為
的體積為![]() 時,求
時,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】國家規(guī)定每年的![]() 月
月![]() 日以后的
日以后的![]() 天為當(dāng)年的暑假.某鋼琴培訓(xùn)機構(gòu)對
天為當(dāng)年的暑假.某鋼琴培訓(xùn)機構(gòu)對![]() 位鋼琴老師暑假一天的授課量進行了統(tǒng)計,如下表所示:
位鋼琴老師暑假一天的授課量進行了統(tǒng)計,如下表所示:
授課量(單位:小時) |
|
|
|
|
|
頻數(shù) |
|
|
|
|
|
培訓(xùn)機構(gòu)專業(yè)人員統(tǒng)計近![]() 年該校每年暑假
年該校每年暑假![]() 天的課時量情況如下表:
天的課時量情況如下表:
課時量(單位:天) |
|
|
|
|
|
頻數(shù) |
|
|
|
|
|
(同組數(shù)據(jù)以這組數(shù)據(jù)的中間值作代表)
(1)估計![]() 位鋼琴老師一日的授課量的平均數(shù);
位鋼琴老師一日的授課量的平均數(shù);
(2)若以(1)中確定的平均數(shù)作為上述一天的授課量.已知當(dāng)?shù)厥谡n價為![]() 元/小時,每天的各類生活成本為
元/小時,每天的各類生活成本為![]() 元/天;若不授課,不計成本,請依據(jù)往年的統(tǒng)計數(shù)據(jù),估計一位鋼琴老師
元/天;若不授課,不計成本,請依據(jù)往年的統(tǒng)計數(shù)據(jù),估計一位鋼琴老師![]() 天暑假授課利潤不少于
天暑假授課利潤不少于![]() 萬元的概率.
萬元的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某市教育局為了監(jiān)控某校高一年級的素質(zhì)教育過程,從該校高一年級16個班隨機抽取了16個樣本成績,制表如下:
抽取次序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
測評成績 | 95 | 96 | 96 | 90 | 95 | 98 | 98 | 97 |
抽取次序 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
測評成績 | 97 | 95 | 96 | 98 | 99 | 96 | 99 | 96 |
令![]() 為抽取的第
為抽取的第![]() 個學(xué)生的素質(zhì)教育測評成績,
個學(xué)生的素質(zhì)教育測評成績,![]() ,經(jīng)計算得,
,經(jīng)計算得,![]() ,
,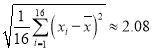 .以下計算精確到0.01.
.以下計算精確到0.01.
(1)設(shè)![]() 為抽取的16個樣本的成績,用頻率估計概率,求
為抽取的16個樣本的成績,用頻率估計概率,求![]() 的分布列、數(shù)學(xué)期望
的分布列、數(shù)學(xué)期望![]() 和標(biāo)準(zhǔn)方差
和標(biāo)準(zhǔn)方差![]() ;
;
(2)在抽取的樣本成績中,如果出現(xiàn)了在![]() 之外的成績,就認為本學(xué)期的素質(zhì)教育過程可能出現(xiàn)了異常情況,需對本學(xué)期的素質(zhì)教學(xué)過程進行反思,同時對下學(xué)期的素質(zhì)教育過程提出指導(dǎo)性的建議.從該校抽樣的結(jié)果來看,是否需對本學(xué)期的素質(zhì)教學(xué)過程進行反思,同時對下學(xué)期的素質(zhì)教育過程提出指導(dǎo)性的建議?
之外的成績,就認為本學(xué)期的素質(zhì)教育過程可能出現(xiàn)了異常情況,需對本學(xué)期的素質(zhì)教學(xué)過程進行反思,同時對下學(xué)期的素質(zhì)教育過程提出指導(dǎo)性的建議.從該校抽樣的結(jié)果來看,是否需對本學(xué)期的素質(zhì)教學(xué)過程進行反思,同時對下學(xué)期的素質(zhì)教育過程提出指導(dǎo)性的建議?
(3)列出不小于![]() 的所有樣本成績,設(shè)列出的這些成績的中位數(shù)為
的所有樣本成績,設(shè)列出的這些成績的中位數(shù)為![]() ,每次從列出的這些成績中隨機抽取1個成績,有放回地連續(xù)抽取3次,求恰好有2次抽得的成績?yōu)?/span>
,每次從列出的這些成績中隨機抽取1個成績,有放回地連續(xù)抽取3次,求恰好有2次抽得的成績?yōu)?/span>![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() :
: ![]() 經(jīng)過橢圓
經(jīng)過橢圓![]() :
: ![]() 的左右焦點
的左右焦點![]() ,且與橢圓
,且與橢圓![]() 在第一象限的交點為
在第一象限的交點為![]() ,且
,且![]() 三點共線,直線
三點共線,直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
, ![]() 兩點,且
兩點,且![]() (
(![]() ).
).
(1)求橢圓![]() 的方程;
的方程;
(2)當(dāng)三角形![]() 的面積取得最大值時,求直線
的面積取得最大值時,求直線![]() 的方程.
的方程.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知動點![]() 到兩點
到兩點![]() ,
,![]() 的距離之和為4,點
的距離之和為4,點![]() 在
在![]() 軸上的射影是C,
軸上的射影是C,![]() .
.
(1)求動點![]() 的軌跡方程;
的軌跡方程;
(2)過點![]() 的直線交點
的直線交點![]() 的軌跡于點
的軌跡于點![]() ,交點
,交點![]() 的軌跡于點
的軌跡于點![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com