
【題目】已知函數![]() .
.
(1)求函數![]() 的單調遞增區間;
的單調遞增區間;
(2)在![]() 中,內角A,B,C所對的邊分別為a,b,c,若
中,內角A,B,C所對的邊分別為a,b,c,若![]() ,求
,求![]() 的面積.
的面積.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用三角函數恒等變換的應用化簡函數解析式可得f(x)=2sin(2x![]() ),利用正弦函數的單調性即可求解其單調遞增區間.
),利用正弦函數的單調性即可求解其單調遞增區間.
(2)由題意可得sin(2A![]() )=1,結合范圍2A
)=1,結合范圍2A![]() ∈(
∈(![]() ,
,![]() ),可求A的值,由正弦定理可得a,由余弦定理b,進而根據三角形的面積公式即可求解.
),可求A的值,由正弦定理可得a,由余弦定理b,進而根據三角形的面積公式即可求解.
(1)∵![]() sin2x﹣cos2x=2sin(2x
sin2x﹣cos2x=2sin(2x![]() ),
),
令2kπ![]() 2x
2x![]() 2kπ
2kπ![]() ,k∈Z,解得kπ
,k∈Z,解得kπ![]() x≤kπ
x≤kπ![]() ,k∈Z,
,k∈Z,
∴函數f(x)的單調遞增區間為:[kπ![]() ,kπ
,kπ![]() ],k∈Z.
],k∈Z.
(2)∵f(A)=2sin(2A![]() )=2,
)=2,
∴sin(2A![]() )=1,
)=1,
∵A∈(0,π),2A![]() ∈(
∈(![]() ,
,![]() ),
),
∴2A![]() ,解得A
,解得A![]() ,
,
∵C![]() ,c=2,
,c=2,
∴由正弦定理![]() ,可得a
,可得a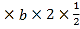 ,
,
∴由余弦定理a2=b2+c2﹣2bccosA,可得6=b2+4﹣2![]() ,解得b=1
,解得b=1![]() ,(負值舍去),
,(負值舍去),
∴S△ABC![]() absinC
absinC![]() (1
(1![]() )
)![]() .
.


 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:高中數學 來源: 題型:
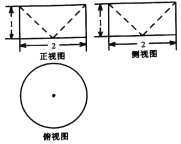
【題目】祖暅是我國南北朝時代的偉大科學家,他在實踐的基礎上提出了體積計算的原理:“冪勢既同,則積不容異”,稱為祖暅原理.意思是底面處于同一平面上的兩個同高的幾何體,若在等高處的截面面積始終相等,則它們的體積相等.利用這個原理求半球O的體積時,需要構造一個幾何體,該幾何體的三視圖如圖所示,則該幾何體的體積為_____,表面積為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
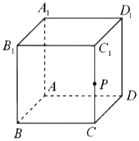
【題目】已知正方體![]() ,點
,點![]() 是棱
是棱![]() 的中點,設直線
的中點,設直線![]() 為
為![]() ,直線
,直線![]() 為
為![]() .對于下列兩個命題:①過點
.對于下列兩個命題:①過點![]() 有且只有一條直線
有且只有一條直線![]() 與
與![]() 、
、![]() 都相交;②過點
都相交;②過點![]() 有且只有一條直線
有且只有一條直線![]() 與
與![]() 、
、![]() 都成
都成![]() 角.以下判斷正確的是( )
角.以下判斷正確的是( )
A.①為真命題,②為真命題B.①為真命題,②為假命題
C.①為假命題,②為真命題D.①為假命題,②為假命題
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知平面內一個動點M到定點F(3,0)的距離和它到定直線l:x=6的距離之比是常數![]() .
.
(1)求動點M的軌跡T的方程;
(2)若直線l:x+y-3=0與軌跡T交于A,B兩點,且線段AB的垂直平分線與T交于C,D兩點,試問A,B,C,D是否在同一個圓上?若是,求出該圓的方程;若不是,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2011年國際數學協會正式宣布,將每年的3月14日設為國際數學節,來源于中國古代數學家祖沖之的圓周率。公元263年,中國數學家劉徽用“割圓術”計算圓周率,計算到圓內接3072邊形的面積,得到的圓周率是![]() .公元480年左右,南北朝時期的數學家祖沖之進一步得出精確到小數點后7位的結果,給出不足近似值3.1415926和過剩近似值3.1415927,還得到兩個近似分數值,密率
.公元480年左右,南北朝時期的數學家祖沖之進一步得出精確到小數點后7位的結果,給出不足近似值3.1415926和過剩近似值3.1415927,還得到兩個近似分數值,密率![]() 和約率
和約率![]() 。大約在公元530年,印度數學大師阿耶波多算出圓周率約為
。大約在公元530年,印度數學大師阿耶波多算出圓周率約為![]() (
(![]() ).在這4個圓周率的近似值中,最接近真實值的是( )
).在這4個圓周率的近似值中,最接近真實值的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】點![]() 是曲線
是曲線![]() :
:![]() 上的一個動點,曲線
上的一個動點,曲線![]() 在點
在點![]() 處的切線與
處的切線與![]() 軸、
軸、![]() 軸分別交于
軸分別交于![]() ,
,![]() 兩點,點
兩點,點![]() 是坐標原點,①
是坐標原點,①![]() ;②
;②![]() 的面積為定值;③曲線
的面積為定值;③曲線![]() 上存在兩點
上存在兩點![]() ,
,![]() 使得
使得![]() 是等邊三角形;④曲線
是等邊三角形;④曲線![]() 上存在兩點
上存在兩點![]() ,
,![]() 使得
使得![]() 是等腰直角三角形,其中真命題的個數是( )
是等腰直角三角形,其中真命題的個數是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國古代數學成就甚大,在世界科技史上占有重要的地位.“算經十書”是漢、唐千余年間陸續出現的10部數學著作,包括《周髀算經》、《九章算術》、……、《綴術》等,它們曾經是隋唐時期國子監算學科的教科書.某中學圖書館全部收藏了這10部著作,其中4部是古漢語本,6部是現代譯本,若某學生要從中選擇2部作為課外讀物,至少有一部是現代譯本的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
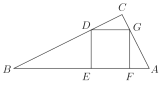
【題目】如圖,已知在Rt△ABC中,![]() ,
,![]() ,
,![]() ,它的內接正方形DEFG的一邊EF在斜邊BA上,D、G分別在邊BC、CA上,設△ABC的面積為
,它的內接正方形DEFG的一邊EF在斜邊BA上,D、G分別在邊BC、CA上,設△ABC的面積為![]() ,正方形DEFG的面積為
,正方形DEFG的面積為![]() .
.
(1)試用![]() 、
、![]() 分別表示
分別表示![]() 和
和![]() ;
;
(2)設![]() ,求
,求![]() 的最大值,并求出此時的
的最大值,并求出此時的![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com