
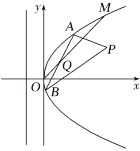
【題目】如圖所示,在直角坐標系![]() 中,點
中,點![]() 到拋物線
到拋物線![]() 的準線的距離為
的準線的距離為![]() .點
.點![]() 是
是![]() 上的定點,
上的定點,![]() ,
,![]() 是
是![]() 上的兩動點,且線段
上的兩動點,且線段![]() 的中點
的中點![]() 在直線
在直線![]() 上.
上.
(Ⅰ)求曲線![]() 的方程及
的方程及![]() 的值;
的值;
(Ⅱ)記![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(Ⅰ)![]() ,
,![]() .(Ⅱ)
.(Ⅱ)![]() .
.
【解析】分析:(Ⅰ)由拋物線準線方程及P到準線的距離,可求得![]() ,進而求得拋物線方程,將點M的坐標代入拋物線 ,即可求得t.
,進而求得拋物線方程,將點M的坐標代入拋物線 ,即可求得t.
(Ⅱ)求直線OM方程,點Q在直線OM上,根據直線方程表示點Q坐標,消去參數n,
利用點差法表示出直線AB斜率,進而求出直線方程,將直線AB方程與拋物線方程聯立,用弦長公式求弦長,從而將d表示為關于m的函數,根據m范圍求最值.
詳解:(1)![]() 的準線為
的準線為![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴拋物線![]() 的方程為
的方程為![]() .又點
.又點![]() 在曲線
在曲線![]() 上,∴
上,∴![]() .
.
(2)由(1)知,點![]() ,從而
,從而![]() ,即點
,即點![]() ,
,
依題意,直線![]() 的斜率存在,且不為
的斜率存在,且不為![]() ,
,
設直線![]() 的斜率為
的斜率為![]() .且
.且![]() ,
,![]() ,
,
由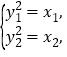 得
得![]() ,故
,故![]() ,
,
所以直線![]() 的方程為
的方程為![]() ,即
,即![]() .
.
由![]() 消去
消去![]() ,整理得
,整理得![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
從而![]() .
.
∴![]() ,
,
當且僅當![]() ,即
,即![]() 時,上式等號成立,
時,上式等號成立,
又![]() 滿足
滿足![]() .∴
.∴![]() 的最大值為
的最大值為![]() .
.


 開心試卷期末沖刺100分系列答案
開心試卷期末沖刺100分系列答案 雙基同步導航訓練系列答案
雙基同步導航訓練系列答案 黃岡小狀元同步計算天天練系列答案
黃岡小狀元同步計算天天練系列答案科目:高中數學 來源: 題型:
【題目】如圖,在五面體ABCDEF中,點O是矩形ABCD的對角線的交點,面CDE是等邊三角形,棱![]() 。
。

(1)證明FO∥平面CDE;
(2)設BC=![]() CD,證明EO⊥平面CDE。
CD,證明EO⊥平面CDE。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司生產甲、乙兩種桶裝產品.已知生產甲產品1桶需耗A原料1千克、B原料2千克;生產乙產品1桶需耗A原料2千克,B原料1千克.每桶甲產品的利潤是300元,每桶乙產品的利潤是400元.公司在生產這兩種產品的計劃中,要求每天消耗A、B原料都不超過12千克.通過合理安排生產計劃,從每天生產的甲、乙兩種產品中,公司共可獲得的最大利潤是( )
A.1800元
B.2400元
C.2800元
D.3100元
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小金同學在學校中貫徹著“邊玩邊學”的學風,他在“漢諾塔”的游戲中發現了數列遞推的奧妙:有![]() 、
、![]() 、
、![]() 三個木樁,
三個木樁,![]() 木樁上套有編號分別為
木樁上套有編號分別為![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 的七個圓環,規定每次只能將一個圓環從一個木樁移動到另一個木樁,且任意一個木樁上不能出現“編號較大的圓環在編號較小的圓環之上”的情況,現要將這七個圓環全部套到
的七個圓環,規定每次只能將一個圓環從一個木樁移動到另一個木樁,且任意一個木樁上不能出現“編號較大的圓環在編號較小的圓環之上”的情況,現要將這七個圓環全部套到![]() 木樁上,則所需的最少次數為( )
木樁上,則所需的最少次數為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠利用隨機數表對生產的600個零件進行抽樣測試,先將600個零件進行編號,編號分別為001,002,![]() ,599,600從中抽取60個樣本,如下提供隨機數表的第4行到第6行:
,599,600從中抽取60個樣本,如下提供隨機數表的第4行到第6行:
32 21 18 34 29 78 64 54 07 32 52 42 06 44 38 12 23 43 56 77 35 78 90 56 42
84 42 12 53 31 34 57 86 07 36 25 30 07 32 86 23 45 78 89 07 23 68 96 08 04
32 56 78 08 43 67 89 53 55 77 34 89 94 83 75 22 53 55 78 32 45 77 89 23 45
若從表中第6行第6列開始向右依次讀取3個數據,則得到的第6個樣本編號![]()
![]()
A. 522B. 324C. 535D. 578
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題:
①函數![]() 的最小正周期是
的最小正周期是![]() ;
;
②在直角坐標系![]() 中,點
中,點![]() ,將向量
,將向量![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 得到向量
得到向量![]() ,則點
,則點![]() 的坐標是
的坐標是![]() ;
;
③在同一直角坐標系中,函數![]() 的圖象和函數
的圖象和函數![]() 的圖象有兩個公共點;
的圖象有兩個公共點;
④函數![]() 在
在![]() 上是增函數.
上是增函數.
其中,正確的命題是________(填正確命題的序號).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】己知數列![]() 是等比數列,且公比為
是等比數列,且公比為![]() ,記
,記![]() 是數列
是數列![]() 的前
的前![]() 項和.
項和.
(1)若![]() =1,
=1,![]() >1,求
>1,求![]() 的值;
的值;
(2)若首項![]() ,
,![]() ,
,![]() 是正整數,滿足不等式|
是正整數,滿足不等式|![]() ﹣63|<62,且
﹣63|<62,且![]() 對于任意正整數
對于任意正整數![]() 都成立,問:這樣的數列
都成立,問:這樣的數列![]() 有幾個?
有幾個?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com