
【題目】在四棱錐![]() 中,平面
中,平面![]()
![]() 平面
平面![]() ,底面
,底面![]() 為梯形,
為梯形,![]() ,
,![]() 且
且![]()
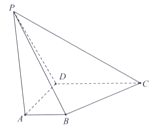
(Ⅰ)求證:![]() ;
;
(Ⅱ)求二面角B-PD-C的余弦值;
(Ⅲ)若M是棱PA的中點(diǎn),求證:對于棱BC上任意一點(diǎn)F,MF與PC都不平行.
【答案】(Ⅰ)見解析;(Ⅱ)![]() ; (Ⅲ)見解析.
; (Ⅲ)見解析.
【解析】
(Ⅰ)利用平面和平面垂直得到線面垂直;
(Ⅱ)利用空間向量求解法向量,從而計算出二面角;
(Ⅲ)利用反證法或者向量求解.
(Ⅰ)在平面![]() 中過點(diǎn)
中過點(diǎn)![]() 作
作![]() ,交
,交![]() 于
于![]()
因為平面![]() 平面
平面![]()
![]() 平面
平面![]()
平面![]() 平面
平面![]()
所以![]() 平面
平面![]()
因為![]() 平面
平面![]()
所以![]()
又![]() ,且
,且![]()
所以![]() 平面
平面![]()
(Ⅱ)因為![]() 平面
平面![]() ,所以
,所以![]()
又![]() ,
,![]()
以![]() 為原點(diǎn),
為原點(diǎn),![]() 所在直線分別為
所在直線分別為![]() 軸,建立空間直角坐標(biāo)系
軸,建立空間直角坐標(biāo)系
所以![]() ,
,
因為![]() 平面
平面![]() ,所以取平面
,所以取平面![]() 的法向量為
的法向量為![]()
設(shè)平面![]() 的法向量為
的法向量為![]()
因為![]() ,所以
,所以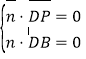
所以![]()
令![]() ,則
,則![]() ,所以
,所以![]()
所以![]()
由題知![]() 為銳角,所以
為銳角,所以![]() 的余弦值為
的余弦值為![]()
(Ⅲ)
法一:
假設(shè)棱![]() 上存在點(diǎn)
上存在點(diǎn)![]() ,使得
,使得![]() ,顯然
,顯然![]() 與點(diǎn)
與點(diǎn)![]() 不同
不同
所以![]() 四點(diǎn)共面于
四點(diǎn)共面于![]()
所以![]()
![]() ,
,![]()
![]()
所以![]()
![]() ,
,![]()
![]()
所以![]() 就是點(diǎn)
就是點(diǎn)![]() 確定的平面,所以
確定的平面,所以![]()
![]()
這與![]() 為四棱錐矛盾,所以假設(shè)錯誤,即問題得證
為四棱錐矛盾,所以假設(shè)錯誤,即問題得證
法二:
假設(shè)棱![]() 上存在點(diǎn)
上存在點(diǎn)![]() ,使得
,使得![]()
連接![]() ,取其中點(diǎn)
,取其中點(diǎn)![]()
在![]() 中,因為
中,因為![]() 分別為
分別為![]() 的中點(diǎn),所以
的中點(diǎn),所以![]()
因為過直線外一點(diǎn)只有一條直線和已知直線平行,所以![]() 與
與![]() 重合
重合
所以點(diǎn)![]() 在線段
在線段![]() 上,所以
上,所以![]() 是
是![]() ,
,![]() 的交點(diǎn)
的交點(diǎn)![]() ,即
,即![]() 就是
就是![]()
而![]() 與
與![]() 相交,矛盾,所以假設(shè)錯誤,問題得證
相交,矛盾,所以假設(shè)錯誤,問題得證
法三:假設(shè)棱![]() 上存在點(diǎn)
上存在點(diǎn)![]() ,使得
,使得![]() ,
,
設(shè)![]() ,所以
,所以![]()
因為![]() ,所以
,所以![]()
所以有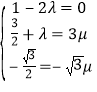 ,這個方程組無解
,這個方程組無解
所以假設(shè)錯誤,即問題得證


 課堂練加測系列答案
課堂練加測系列答案 輕松課堂單元測試AB卷系列答案
輕松課堂單元測試AB卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() ,
,![]() .
.
(1)當(dāng)![]() 時,求
時,求![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)當(dāng)![]() 時,若對任意的
時,若對任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立,求實(shí)數(shù)
成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 。
。
(1)當(dāng)![]() 時,求函數(shù)
時,求函數(shù)![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程;
處的切線方程;
(2)若函數(shù)![]() ,討論函數(shù)
,討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(3)若(2)中函數(shù)![]() 有兩個極值點(diǎn)
有兩個極值點(diǎn)![]()
![]() ,且不等式
,且不等式![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在極坐標(biāo)系中,曲線C1的極坐標(biāo)方程是![]() ,在以極點(diǎn)為原點(diǎn)O,極軸為x軸正半軸(兩坐標(biāo)系取相同的單位長度)的直角坐標(biāo)系xOy中,曲線C2的參數(shù)方程為
,在以極點(diǎn)為原點(diǎn)O,極軸為x軸正半軸(兩坐標(biāo)系取相同的單位長度)的直角坐標(biāo)系xOy中,曲線C2的參數(shù)方程為![]() (θ為參數(shù)).
(θ為參數(shù)).
(1)求曲線C1的直角坐標(biāo)方程與曲線C2的普通方程;
(2)將曲線C2經(jīng)過伸縮變換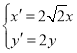 后得到曲線C3,若M,N分別是曲線C1和曲線C3上的動點(diǎn),求|MN|的最小值.
后得到曲線C3,若M,N分別是曲線C1和曲線C3上的動點(diǎn),求|MN|的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某人從上一層到二層需跨10級臺階. 他一步可能跨1級臺階,稱為一階步,也可能跨2級臺階,稱為二階步,最多能跨3級臺階,稱為三階步. 從一層上到二層他總共跨了6步,而且任何相鄰兩步均不同階. 則他從一層到二層可能的不同過程共有( )種.
A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本小題滿分14分)
已知數(shù)列![]() 是首項為1,公比為2的等比數(shù)列,數(shù)列
是首項為1,公比為2的等比數(shù)列,數(shù)列![]() 的前
的前![]() 項和
項和![]() .
.
(1)求數(shù)列![]() 與
與![]() 的通項公式;
的通項公式;
(2)求數(shù)列![]() 的前
的前![]() 項和.
項和.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() :
:![]() ,圓
,圓![]() 關(guān)于直線
關(guān)于直線![]() 對稱,圓心在第二象限,半徑為
對稱,圓心在第二象限,半徑為![]() .
.
(1)求圓![]() 的方程;
的方程;
(2)直線![]() 與圓
與圓![]() 相切,且在
相切,且在![]() 軸、
軸、![]() 軸上的截距相等,求直線
軸上的截距相等,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2018年國際象棋奧林匹克團(tuán)體賽中國男隊、女隊同時奪冠.國際象棋中騎士的移動規(guī)則是沿著3×2格或2×3格的對角移動.在歷史上,歐拉、泰勒、哈密爾頓等數(shù)學(xué)家研究了“騎士巡游”問題:在![]() 格的黑白相間的國際象棋棋盤上移動騎士,是否可以讓騎士從某方格內(nèi)出發(fā)不重復(fù)地走遍棋盤上的每一格?
格的黑白相間的國際象棋棋盤上移動騎士,是否可以讓騎士從某方格內(nèi)出發(fā)不重復(fù)地走遍棋盤上的每一格?
圖(一)給出了騎士的一種走法,它從圖上標(biāo)1的方格內(nèi)出發(fā),依次經(jīng)過標(biāo)2,3,4,5,6,![]() ,到達(dá)標(biāo)64的方格內(nèi),不重復(fù)地走遍棋盤上的每一格,又可從標(biāo)64的方格內(nèi)直接走回到標(biāo)1的方格內(nèi).如果騎士的出發(fā)點(diǎn)在左下角標(biāo)50的方格內(nèi),按照上述走法,_____(填“能”或“不能”)走回到標(biāo)50的方格內(nèi).
,到達(dá)標(biāo)64的方格內(nèi),不重復(fù)地走遍棋盤上的每一格,又可從標(biāo)64的方格內(nèi)直接走回到標(biāo)1的方格內(nèi).如果騎士的出發(fā)點(diǎn)在左下角標(biāo)50的方格內(nèi),按照上述走法,_____(填“能”或“不能”)走回到標(biāo)50的方格內(nèi).
若騎士限制在圖(二)中的3×4=12格內(nèi)按規(guī)則移動,存在唯一一種給方格標(biāo)數(shù)字的方式,使得騎士從左上角標(biāo)1的方格內(nèi)出發(fā),依次不重復(fù)經(jīng)過2,3,4,5,6,![]() ,到達(dá)右下角標(biāo)12的方格內(nèi),分析圖(二)中A處所標(biāo)的數(shù)應(yīng)為____.
,到達(dá)右下角標(biāo)12的方格內(nèi),分析圖(二)中A處所標(biāo)的數(shù)應(yīng)為____.
35 | 38 | 27 | 16 | 29 | 42 | 55 | 18 |
26 | 15 | 36 | 39 | 54 | 17 | 30 | 43 |
37 | 34 | 13 | 28 | 41 | 32 | 19 | 56 |
14 | 25 | 40 | 33 | 20 | 53 | 44 | 31 |
63 | 12 | 21 | 52 | 1 | 8 | 57 | 46 |
24 | 51 | 64 | 9 | 60 | 45 | 2 | 5 |
11 | 62 | 49 | 22 | 7 | 4 | 47 | 58 |
50 | 23 | 10 | 61 | 48 | 59 | 6 | 3 |
圖(一)
1 | |||
A | |||
3 | 12 |
圖(二)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
![]() Ⅰ
Ⅰ![]() 當(dāng)
當(dāng)![]() 時,
時,![]() 取得極值,求
取得極值,求![]() 的值并判斷
的值并判斷![]() 是極大值點(diǎn)還是極小值點(diǎn);
是極大值點(diǎn)還是極小值點(diǎn);
![]() Ⅱ
Ⅱ![]() 當(dāng)函數(shù)
當(dāng)函數(shù)![]() 有兩個極值點(diǎn)
有兩個極值點(diǎn)![]() ,
,![]() ,且
,且![]() 時,總有
時,總有![]() 成立,求
成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com