
【題目】若函數g(x)滿足g(g(x))=n(n∈N)有n+3個解,則稱函數g(x)為“復合n+3解”函數.已知函數f(x)= 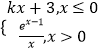 (其中e是自然對數的底數,e=2.71828…,k∈R),且函數f(x)為“復合5解”函數,則k的取值范圍是( )
(其中e是自然對數的底數,e=2.71828…,k∈R),且函數f(x)為“復合5解”函數,則k的取值范圍是( )
A.(﹣∞,0)
B.(﹣e,e)
C.(﹣1,1)
D.(0,+∞)
【答案】D
【解析】解:函數f(x)為“復合5解“, ∴f(f(x))=2,有5個解,
設t=f(x),
∴f(t)=2,
∵當x>0時,f(x)= ![]() ,
,
∴f(x)= ![]() ,
,
當0<x<1時,f′(x)<0,函數f(x)單調遞減,
當x>1時,f′(x)>0,
函數f(x)單調遞增,
∴f(x)min=f(1)=1,
∴t≥1,
∴f(t)=2在[1,+∞)有2個解,
當x≤0時,f(x)=kx+3,函數f(x)恒過點(0,3),
當k≤0時,f(x)≥f(0)=3,
∴t≥3
∵f(3)= ![]() >2,
>2,
∴f(t)=2在[3,+∞)上無解,
當k>0時,f(x)≤f(0)=3,
∴f(t)=2,在(0,3]上有2個解,在(∞,0]上有1個解,
綜上所述f(f(x))=2在k>0時,有5個解,
故選:D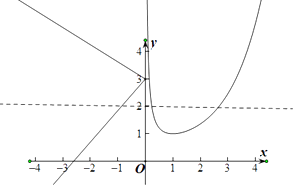


科目:高中數學 來源: 題型:
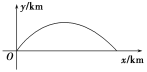
【題目】如圖,建立平面直角坐標系,x軸在地平面上,y軸垂直于地平面,單位長度為1 km,某炮位于原點.已知炮彈發射后的軌跡在方程y=kx-![]() (1+k2)x2(k>0)表示的曲線上,其中k與發射方向有關.炮的射程是指炮彈落地點的橫坐標.則炮的最大射程為( )
(1+k2)x2(k>0)表示的曲線上,其中k與發射方向有關.炮的射程是指炮彈落地點的橫坐標.則炮的最大射程為( )
A. 20 km B. 10 km
C. 5 km D. 15 km
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知一次函數f(x)=ax-2.
(1)當a=3時,解不等式|f(x)|<4;
(2)解關于x的不等式|f(x)|<4;
(3)若關于x的不等式|f(x)|≤3對任意x∈[0,1]恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對某校高一年級學生參加社區服務次數進行統計,隨機抽取M名學生作為樣本,得到這M名學生參加社區服務的次數.根據此數據作出了頻數與頻率的統計表和頻率分布直方圖如下:
分組 | 頻數 | 頻率 |
[10,15) | 10 | 0.25 |
[15,20) | 25 | n |
[20,25) | m | p |
[25,30) | 2 | 0.05 |
合計 | M | 1 |
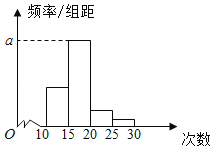
(1)求出表中M,p及圖中a的值;
(2)若該校高一學生有360人,試估計該校高一學生參加社區服務的次數在區間[15,20)內的人數;
(3)在所取樣本中,從參加社區服務的次數不少于20次的學生中任選2人,請列舉出所有基本事件,并求至多1人參加社區服務次數在區間[20,25)內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
在直角坐標系xOy中,直線l的參數方程為 ![]() (t為參數),在以O為極點x軸的非負半軸為極軸建立的極坐標系中,曲線C的極坐標方程為ρ=2.
(t為參數),在以O為極點x軸的非負半軸為極軸建立的極坐標系中,曲線C的極坐標方程為ρ=2.
(1)求直線l的普通方程和曲線C的直角坐標方程;
(2)若點Q是曲線C上的動點,求點Q到直線l的距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是橢圓
是橢圓![]() 與拋物線
與拋物線![]() 的一個公共點,且橢圓與拋物線具有一個相同的焦點
的一個公共點,且橢圓與拋物線具有一個相同的焦點![]() .
.
(1)求橢圓![]() 及拋物線
及拋物線![]() 的方程;
的方程;
(2)設過![]() 且互相垂直的兩動直線
且互相垂直的兩動直線![]() ,
,![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,
兩點,![]() 與拋物線
與拋物線![]() 交于
交于![]() 兩點,求四邊形
兩點,求四邊形![]() 面積的最小值
面積的最小值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,小明想將短軸長為2,長軸長為4的一個半橢圓形紙片剪成等腰梯形ABDE,且梯形ABDE內接于半橢圓,DE∥AB,AB為短軸,OC為長半軸
(1)求梯形ABDE上底邊DE與高OH長的關系式;
(2)若半橢圓上到H的距離最小的點恰好為C點,求底邊DE的取值范圍

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以下三個關于圓錐曲線的命題中:
①設![]() 為兩個定點,
為兩個定點,![]() 為非零常數,若
為非零常數,若![]() ,則動點
,則動點![]() 的軌跡是雙曲線;
的軌跡是雙曲線;
②方程![]() 的兩根可分別作為橢圓和雙曲線的離心率;
的兩根可分別作為橢圓和雙曲線的離心率;
③雙曲線![]() 與橢圓
與橢圓![]() 有相同的焦點;
有相同的焦點;
④已知拋物線![]() ,以過焦點的一條弦
,以過焦點的一條弦![]() 為直徑作圓,則此圓與準線相切,其中真命題為__________.(寫出所有真命題的序號)
為直徑作圓,則此圓與準線相切,其中真命題為__________.(寫出所有真命題的序號)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com