
【題目】已知函數f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ< ![]() )的部分圖象如圖所示.
)的部分圖象如圖所示. 
(1)求函數f(x)的解析式;
(2)求函數g(x)=f(x﹣ ![]() )﹣f(x+
)﹣f(x+ ![]() )的單調遞增區間.
)的單調遞增區間.
【答案】
(1)解:由圖象可知,周期T=2( ![]() ﹣
﹣ ![]() )=π,∴ω=
)=π,∴ω= ![]() =2
=2
∵點( ![]() ,0)在函數圖象上,∴Asin(2×
,0)在函數圖象上,∴Asin(2× ![]() +φ)=0
+φ)=0
∴sin( ![]() +φ)=0,∴
+φ)=0,∴ ![]() +φ=π+kπ,即φ=kπ+
+φ=π+kπ,即φ=kπ+ ![]() ,k∈z
,k∈z
∵0<φ< ![]()
∴φ= ![]()
∵點(0,1)在函數圖象上,∴Asin ![]() =1,A=2
=1,A=2
∴函數f(x)的解析式為f(x)=2sin(2x+ ![]() )
)
(2)解:g(x)=2sin[2(x﹣ ![]() )+
)+ ![]() ]﹣2sin[2(x+
]﹣2sin[2(x+ ![]() )+
)+ ![]() ]=2sin2x﹣2sin(2x+
]=2sin2x﹣2sin(2x+ ![]() )
)
=2sin2x﹣2( ![]() sin2x+
sin2x+ ![]() cos2x)=sin2x﹣
cos2x)=sin2x﹣ ![]() cos2x
cos2x
=2sin(2x﹣ ![]() )
)
由﹣ ![]() +2kπ≤2x﹣
+2kπ≤2x﹣ ![]() ≤
≤ ![]() +2kπ,k∈z
+2kπ,k∈z
得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]()
∴函數g(x)=f(x﹣ ![]() )﹣f(x+
)﹣f(x+ ![]() )的單調遞增區間為[kπ﹣
)的單調遞增區間為[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ]k∈z
]k∈z
【解析】(1)先利用函數圖象求此函數的周期,從而計算得ω的值,再將點( ![]() ,0)和(0,1)代入解析式,分別解得φ和A的值,最后寫出函數解析式即可;(2)先利用三角變換公式將函數g(x)的解析式化為y=Asin(ωx+φ)型函數,再將內層函數看做整體,置于外層函數即正弦函數的單調增區間上,即可解得函數g(x)的單調增區間
,0)和(0,1)代入解析式,分別解得φ和A的值,最后寫出函數解析式即可;(2)先利用三角變換公式將函數g(x)的解析式化為y=Asin(ωx+φ)型函數,再將內層函數看做整體,置于外層函數即正弦函數的單調增區間上,即可解得函數g(x)的單調增區間


 開心蛙狀元作業系列答案
開心蛙狀元作業系列答案 課時掌控隨堂練習系列答案
課時掌控隨堂練習系列答案 一課一練一本通系列答案
一課一練一本通系列答案 浙江之星學業水平測試系列答案
浙江之星學業水平測試系列答案科目:高中數學 來源: 題型:
【題目】如圖,在直角坐標系![]() 中,圓
中,圓![]() 與
與![]() 軸負半軸交于點
軸負半軸交于點![]() ,過點
,過點![]() 的直線
的直線![]() ,
,![]() 分別與圓
分別與圓![]() 交于
交于![]() ,
,![]() 兩點.
兩點.

(Ⅰ)若![]() ,
,![]() ,求
,求![]() 的面積;
的面積;
(Ⅱ)若直線![]() 過點
過點![]() ,證明:
,證明:![]() 為定值,并求此定值.
為定值,并求此定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“微信運動”已成為當下熱門的健身方式,小王的微信朋友圈內也有大量好友參與了“微信運動”,他隨機選取了其中的40人(男、女各20人),記錄了他們某一天的走路步數,并將數據整理如下:
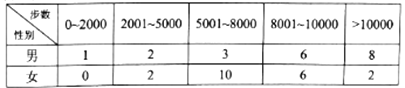
(1)若采用樣本估計總體的方式,試估計小王的所有微信好友中每日走路步數超過5000步的概率;
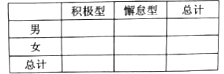
(2)已知某人一天的走路步數超過8000步被系統評定“積極型”,否則為“懈怠型”,根據題意完成下面的![]() 列聯表,并據此判斷能否有95%以上的把握認為“評定類型”與“性別”有關?
列聯表,并據此判斷能否有95%以上的把握認為“評定類型”與“性別”有關?
 附:
附: 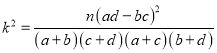 ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin(ωx+φ),x∈R(其中 ![]() )的圖象與x軸的交點中,相鄰兩個交點之間的距離為
)的圖象與x軸的交點中,相鄰兩個交點之間的距離為 ![]() ,且圖象上一個最低點為
,且圖象上一個最低點為 ![]() .
.
(1)求f(x)的解析式;
(2)當 ![]() ,求f(x)的值域.
,求f(x)的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知,圓C:x2+y2﹣8y+12=0,直線l:ax+y+2a=0.
(1)當a為何值時,直線l與圓C相切;
(2)當直線l與圓C相交于A、B兩點,且AB=2 ![]() 時,求直線l的方程.
時,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲乙兩人玩猜數字游戲,先由甲心中任想一個數字記為![]() ,再由乙猜甲剛才想的數字,把乙猜的數字記為
,再由乙猜甲剛才想的數字,把乙猜的數字記為![]() ,且
,且![]() 、
、![]() .若
.若![]() ,則稱甲乙“心有靈犀”.現任意找兩人玩這個游戲,則二人“心有靈犀”的概率為__________.
,則稱甲乙“心有靈犀”.現任意找兩人玩這個游戲,則二人“心有靈犀”的概率為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是函數![]() 的圖象,給出下列命題:
的圖象,給出下列命題:

①![]() 是函數
是函數![]() 的極值點
的極值點
②1是函數![]() 的極小值點
的極小值點
③![]() 在
在![]() 處切線的斜率大于零
處切線的斜率大于零
④![]() 在區間
在區間![]() 上單調遞減
上單調遞減
則正確命題的序號是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】把函數y=sin(2x+ ![]() )的圖象向右平移
)的圖象向右平移 ![]() 個單位,再把所得圖象上各點的橫坐標縮短到原來的
個單位,再把所得圖象上各點的橫坐標縮短到原來的 ![]() ,則所得圖象的函數解析式是( )
,則所得圖象的函數解析式是( )
A.y=sin(4x+ ![]() π)
π)
B.y=sin(4x+ ![]() )
)
C.y=sin4x
D.y=sinx
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com