精英家教網(wǎng)> 2025年暑假生活八年級數(shù)學(xué)河北少年兒童出版社 > 第1頁 參考答案
2025年暑假生活八年級數(shù)學(xué)河北少年兒童出版社
注:目前有些書本章節(jié)名稱可能整理的還不是很完善,但都是按照順序排列的,請同學(xué)們按照順序仔細(xì)查找。練習(xí)冊2025年暑假生活八年級數(shù)學(xué)河北少年兒童出版社答案主要是用來給同學(xué)們做完題方便對答案用的,請勿直接抄襲。
1. 使式子$\sqrt {2x+1}$在實數(shù)范圍內(nèi)有意義的x的取值范圍是
$x \geq -\frac{1}{2}$
.
答案:【解析】:
為了使$\sqrt{2x+1}$在實數(shù)范圍內(nèi)有意義,被開方數(shù)$2x+1$必須是非負(fù)數(shù)。
因此,我們設(shè)置不等式:
$2x + 1 \geq 0$
解這個不等式,我們得到:
$2x \geq -1$
$x \geq -\frac{1}{2}$
【答案】:
$x \geq -\frac{1}{2}$
2. 在一次函數(shù)$y= (2-k)x+1$中,若$y隨x$的增大而增大,則$k$的取值范圍為______
$k<2$
.
答案:【解析】:對于一次函數(shù)$y = mx + b$($m$、$b$為常數(shù),$m\neq0$),當(dāng)$m>0$時,$y$隨$x$的增大而增大。在函數(shù)$y=(2 - k)x + 1$中,斜率$m = 2 - k$。因為$y$隨$x$的增大而增大,所以$2 - k>0$,解這個不等式可得$k<2$。
【答案】:$k<2$
3. 在一個四邊形中,最多能有
3
個銳角,最多能有
3
個鈍角.
答案:【解析】:對于四邊形中銳角的個數(shù),因為銳角是小于$90^{\circ}$的角,假設(shè)四邊形有$4$個銳角,那么四個內(nèi)角之和會小于$4×90^{\circ}=360^{\circ}$,這與四邊形內(nèi)角和是$360^{\circ}$矛盾;若有$3$個銳角,設(shè)這$3$個銳角都接近$90^{\circ}$,比如都為$89^{\circ}$,則第四個角為$360^{\circ}-3×89^{\circ}=360^{\circ}-267^{\circ}=93^{\circ}$,是合理的,所以最多有$3$個銳角。
對于鈍角的個數(shù),鈍角是大于$90^{\circ}$小于$180^{\circ}$的角,假設(shè)四邊形有$4$個鈍角,那么四個內(nèi)角之和會大于$4×90^{\circ}=360^{\circ}$且小于$4×180^{\circ}=720^{\circ}$,但四邊形內(nèi)角和固定為$360^{\circ}$,$4$個鈍角之和必然大于$360^{\circ}$,矛盾;若有$3$個鈍角,設(shè)這$3$個鈍角都接近$180^{\circ}$,比如都為$91^{\circ}$,則第四個角為$360^{\circ}-3×91^{\circ}=360^{\circ}-273^{\circ}=87^{\circ}$,是合理的,所以最多有$3$個鈍角。
【答案】:3,3
4. 某班圍繞“舞蹈、樂器、聲樂、其他項目中,你最喜歡哪項活動(每人只限選一項)”的問題,對全班50名學(xué)生進行問卷調(diào)查,調(diào)查結(jié)果如圖1-1所示的扇形統(tǒng)計圖,則該班喜歡樂器的學(xué)生有
22
名.
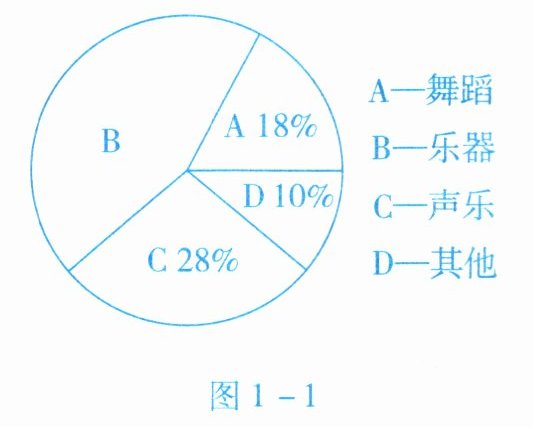
答案:【解析】:根據(jù)扇形統(tǒng)計圖可知,喜歡樂器的學(xué)生所占比例為:
$1 - 18\% - 28\% - 10\% = 44\%$。
該班學(xué)生總?cè)藬?shù)為$50$名,所以喜歡樂器的學(xué)生人數(shù)為:
$50× 44\% = 50×0.44 = 22$(名)。
【答案】:$22$
5. 如圖$1-2$所示,在矩形$ABCD$中,對角線$AC$,$BD相交于點O$,點$E$,$F分別是AO$,$AD$的中點. 若$AB= 6cm$,$BC= 8cm$,則$\triangle AEF$的周長為______
9
$cm$.
答案:【解析】:
首先,由于$ABCD$是矩形,所以根據(jù)勾股定理,有$AC = \sqrt{AB^2 + BC^2} = \sqrt{6^2 + 8^2} = 10 \text{ cm}$。
由于$O$是對角線$AC$和$BD$的交點,根據(jù)矩形的性質(zhì),$O$是$AC$的中點,所以$AO = \frac{AC}{2} = 5 \text{ cm}$。
點$E$是$AO$的中點,所以$AE = \frac{AO}{2} = 2.5 \text{ cm}$。
點$F$是$AD$的中點,由于$AD = BC = 8 \text{ cm}$,所以$AF = \frac{AD}{2} = 4 \text{ cm}$。
由于$E$和$F$分別是$AO$和$AD$的中點,根據(jù)中位線的性質(zhì),$EF$是$\triangle AOD$的中位線,所以$EF = \frac{1}{2}OD = \frac{1}{2} × \frac{1}{2}BD = \frac{1}{4}AC = 2.5 \text{ cm}$(這里用到了$OD = \frac{1}{2}BD$和$BD = AC$)。
最后,$\triangle AEF$的周長為$AE + AF + EF = 2.5 + 4 + 2.5 = 9 \text{ cm}$。
【答案】:9
1. 矩形的兩條對角線的夾角是$120^{\circ }$,較短的邊長是$4cm$,則其較長的邊長是(
C
)
A.$8\sqrt {3}cm$
B.$8cm$
C.$4\sqrt {3}cm$
D.$4cm$
答案:【解析】:在矩形中,對角線相等且互相平分,所以兩條對角線與矩形兩邊構(gòu)成的三角形中,兩條對角線的一半相等。已知兩條對角線的夾角是$120^{\circ}$,則其鄰補角為$60^{\circ}$。較短的邊長與兩條對角線的一半構(gòu)成一個等邊三角形(因為夾角為$60^{\circ}$且兩邊相等),所以對角線的一半等于較短邊長$4cm$,則對角線長為$8cm$。
設(shè)較長的邊長為$x cm$,根據(jù)勾股定理,較短邊、較長邊與對角線構(gòu)成直角三角形,可得:$4^{2} + x^{2} = 8^{2}$,即$16 + x^{2} = 64$,解得$x^{2} = 48$,$x = 4\sqrt{3}$(負(fù)值舍去)。
【答案】:C
2. 下列計算錯誤的是(
B
)
A.$\sqrt {2}\cdot \sqrt {3}= \sqrt {6}$
B.$\sqrt {2}+\sqrt {3}= \sqrt {6}$
C.$\sqrt {12}÷ \sqrt {3}= 2$
D.$\sqrt {8}= 2\sqrt {2}$
答案:【解析】:逐一分析各選項:
選項A:根據(jù)二次根式乘法法則,$\sqrt{a} \cdot \sqrt{b} = \sqrt{ab}$($a\geq0$,$b\geq0$),所以$\sqrt{2} \cdot \sqrt{3} = \sqrt{2×3} = \sqrt{6}$,計算正確。
選項B:$\sqrt{2}$和$\sqrt{3}$不是同類二次根式,不能直接合并,$\sqrt{2} + \sqrt{3}$已是最簡形式,不能等于$\sqrt{6}$,計算錯誤。
選項C:根據(jù)二次根式除法法則,$\sqrt{a} ÷ \sqrt{b} = \sqrt{\frac{a}{b}}$($a\geq0$,$b>0$),所以$\sqrt{12} ÷ \sqrt{3} = \sqrt{\frac{12}{3}} = \sqrt{4} = 2$,計算正確。
選項D:$\sqrt{8} = \sqrt{4×2} = \sqrt{4} \cdot \sqrt{2} = 2\sqrt{2}$,計算正確。
綜上,計算錯誤的是選項B。
【答案】:B

