
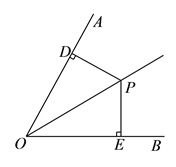
【題目】已知:如圖, ![]() 是
是![]() 內一點,
內一點, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別是垂足,且
分別是垂足,且![]() .
.
(![]() )求證:點
)求證:點![]() 在
在![]() 的平分線上.
的平分線上.
(![]() )若點
)若點![]() 是射線
是射線![]() 上一點,點
上一點,點![]() 是射線
是射線![]() 上一點,且
上一點,且![]() ,
, ![]() .
.
①當![]() 是等腰三角形時,求點
是等腰三角形時,求點![]() 到射線
到射線![]() 的距離;
的距離;
②連接![]() ,
, ![]() ,
, ![]() ,當
,當![]() 的周長最小時,求
的周長最小時,求![]() 的度數.
的度數.
【答案】(![]() )證明見解析;(
)證明見解析;(![]() )①
)①![]() 或
或![]() 或
或![]() ;②
;②![]() .
.
【解析】試題分析:(1)證明![]() ≌
≌![]() ,根據全等三角形的對應角相等即可得;
,根據全等三角形的對應角相等即可得;
(2)①分![]() 或
或![]() 或
或![]() 三種情況進行討論即可得;
三種情況進行討論即可得;
②當![]() 為等邊三角形時,
為等邊三角形時, ![]() 周長最小,則
周長最小,則![]() .作點
.作點![]() 關于射線
關于射線![]() 的對應點
的對應點![]() ,關于射線
,關于射線![]() 的一應點
的一應點![]() ,連結
,連結![]()
![]() ,則線段
,則線段![]()
![]() 與
與![]() 的交點為
的交點為![]() .與
.與![]() 的交點為
的交點為![]() ,連結
,連結![]() ,
, ![]() ,
, ![]() ,由兩點之間線段最短,可知
,由兩點之間線段最短,可知![]() 周小.
周小.
試題解析:(1)在![]() 和
和![]() 中,有
中,有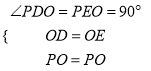 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∴![]() 在
在![]() 的平分線上;
的平分線上;
(2)①若![]() 是等腰三角形,則
是等腰三角形,則![]() 或
或![]() 或
或![]() .
.
(Ⅰ)若![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
又![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
, ![]() ,
, ![]() 三點共線.
三點共線.
∴![]() 到
到![]() 的距離為
的距離為![]() ;
;
(Ⅱ)若![]() ,過點
,過點![]() 作
作![]() ,垂足為
,垂足為![]() ,連結
,連結![]() .
.
∵![]() ,則
,則![]() ,
,
∴![]() .
.
∴![]() .
.
又![]() ,設
,設![]() ,
,
則![]() ,
,
即![]() .
.
在![]() 中,
中, ![]() ,
,
∴![]() .
.
在![]() 中,
中, ![]() ,
,
∴![]() ;
;
(Ⅲ)若![]() ,同理可知
,同理可知![]() .
.
綜上,點![]() 到射線
到射線![]() 的距離為
的距離為![]() 或
或![]() 或
或![]() ;
;
②當![]() 為等邊三角形時,
為等邊三角形時, ![]() 周長最小,則
周長最小,則![]() .
.
作點![]() 關于射線
關于射線![]() 的對應點
的對應點![]() ,關于射線
,關于射線![]() 的一應點
的一應點![]() ,連結
,連結![]()
![]() ,則線段
,則線段![]()
![]() 與
與![]() 的交點為
的交點為![]() .與
.與![]() 的交點為
的交點為![]() ,連結
,連結![]() ,
, ![]() ,
, ![]() ,由兩點之間線段最短,可知
,由兩點之間線段最短,可知![]() 周小.
周小.
如圖所示:由軸對稱性質可得,
OP1=OP2=OP,∠P1OA=∠POA,∠P2OB=∠POB,
所以∠P1OP2=2∠AOB=2×60°=120°,
所以∠OP1P2=∠OP2P1=(180°-120°)÷2=30°,
又因為∠FPO=∠OP1F=30°,∠GPO=∠OP2G=30°,
所以∠FPG=∠FPO+∠GPO=60°.



科目:初中數學 來源: 題型:
【題目】有質地均勻的A、B、C、D四張卡片,上面對應的圖形分別是圓、正方形、正三角形、平行四邊形,將這四張卡片放入不透明的盒子中搖勻,從中隨機抽出一張(不放回),再隨機抽出第二張.
(1)如果要求抽出的兩張卡片上的圖形,既有圓又有三角形,請你用列表或畫樹狀圖的方法,求出出現這種情況的概率;
(2)因為四張卡片上有兩張上的圖形,既是中心對稱圖形,又是軸對稱圖形,所以小明和小東約定做一個游戲,規則是:如果抽出的兩個圖形,既是中心對稱圖形又是軸對稱圖形,則小明贏;否則,小東贏.問這個游戲公平嗎?為什么?如果不公平,請你設計一個公平的游戲規則.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】PM2.5是指大氣中直徑小于或等于2.5微米的顆粒,已知米=1000000微米,則2.5微米=0.0000025米,用科學記數法可以表示為_____米.
查看答案和解析>>
科目:初中數學 來源: 題型:
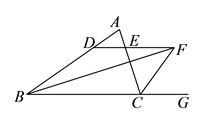
【題目】如圖,在![]() 中,
中, ![]() ,
, ![]() 的平分線
的平分線![]() 與
與![]() 的外角平分線交于點
的外角平分線交于點![]() ,過點
,過點![]() 作
作![]() ,交
,交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() .
.
(![]() )圖中除
)圖中除![]() 之外,還有幾個等腰三角形,請分別寫出來;
之外,還有幾個等腰三角形,請分別寫出來;
(![]() )若
)若![]() ,
, ![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有兩個可以自由轉動的均勻轉盤![]() ,都被分成了3等份,并在每份內均標有數字,如圖所示.規則如下:
,都被分成了3等份,并在每份內均標有數字,如圖所示.規則如下:
①分別轉動轉盤![]() ;
;
②兩個轉盤停止后,將兩個指針所指份內的數字相乘(若指針停止在等份線上,那么重轉一次,直到指針指向某一份為止).

【1】用列表法或樹狀圖分別求出數字之積為3的倍數和數字之積為5的倍數的概率;
【2】小明和小亮想用這兩個轉盤做游戲,他們規定:數字之積為3的倍數時,小明得2分;數字之積為5的倍數時,小亮得3分.這個游戲對雙方公平嗎?請說明理由;認為不公平的,試修改得分規定,使游戲對雙方公平.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,∠ACB=90°,BD是△ABC的角平分線,P是射線AC上任意一點 (不與A、D、C三點重合),過點P作PQ⊥AB,垂足為Q,交線段BD于E.
(1)如圖①,當點P在線段AC上時,說明∠PDE=∠PED.
(2)畫出∠CPQ的角平分線交線段AB于點F,則PF與BD有怎樣的位置關系?畫出圖形并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示的方格紙中每個小方格都是邊長為1個單位長度的正方形,在平面直角坐標系中,已知點A(0,-1),B(0,3),C(-3,2).
(1) 描出A、B、C三點的位置,并畫出三角形ABC;
(2) 三角形ABC中任意一點P(x,y)平移后的對應點為P1(x+3,y-2)將三角形ABC作同樣的平移得到三角形A1B1C1,作出平移后的圖形,并寫出點A1、B1、C1的坐標;
(3) 求三角形A1B1C1的面積.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com