
【題目】如圖,△ABC在直角坐標系中,
(1)請寫出△ABC各點的坐標.
(2)若把△ABC向上平移2個單位,再向左平移1個單位得到△A′B′C′,寫出 A′、B′、C′的坐標,并在圖中畫出平移后圖形.
(3)求出三角形ABC的面積.

【答案】(1)A(﹣2,﹣2),B (3,1),C(0,2);(2)圖形見解析,A′(﹣3,0)、B′(2,3),C′(﹣1,4);(3)7.
【解析】分析:(1)根據(jù)平面直角坐標系寫出各點的坐標即可;(2)根據(jù)網(wǎng)格結(jié)構(gòu)找出點A、B、C平移后的對應點A′、B′、C′的位置,然后順次連接即可,再根據(jù)平面直角坐標系寫出點A′、B′、C′的坐標;(3)利用△ABC所在的矩形的面積減去四周三個直角三角形的面積,列式計算即可得解.
本題解析:
(1)A(﹣2,﹣2),B (3,1),C(0,2);
(2)△A′B′C′如圖所示,
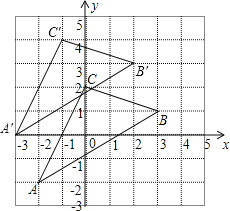
A′(﹣3,0)、B′(2,3),C′(﹣1,4);
(3)△ABC的面積=5×4﹣![]() ×2×4﹣
×2×4﹣![]() ×5×3﹣
×5×3﹣![]() ×1×3=20﹣4﹣7.5﹣1.5=20﹣13=7 .故答案為:(1)A(﹣2,﹣2),B (3,1),C(0,2);(2)作圖見解析;A′(﹣3,0)、B′(2,3),C′(﹣1,4);(3)7.
×1×3=20﹣4﹣7.5﹣1.5=20﹣13=7 .故答案為:(1)A(﹣2,﹣2),B (3,1),C(0,2);(2)作圖見解析;A′(﹣3,0)、B′(2,3),C′(﹣1,4);(3)7.


 探究與鞏固河南科學技術(shù)出版社系列答案
探究與鞏固河南科學技術(shù)出版社系列答案科目:初中數(shù)學 來源: 題型:
【題目】當﹣2≤x≤1時,二次函數(shù)y=﹣(x﹣m)2+m2+1有最大值4,則實數(shù)m的值為( )
A.﹣ ![]()
B.![]() 或﹣
或﹣ ![]()
C.2或﹣ ![]()
D.2或﹣ ![]() 或﹣
或﹣ ![]()
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點A,B的坐標分別為A(![]() ,0),B(
,0),B(![]() ,0),且
,0),且![]() 、
、![]() 滿足
滿足![]() ,現(xiàn)同時將點A,B分別向上平移2個單位,再向右平移1個單位,分別得到點A,B的對應點C,D,連接AC,BD,CD.
,現(xiàn)同時將點A,B分別向上平移2個單位,再向右平移1個單位,分別得到點A,B的對應點C,D,連接AC,BD,CD.

(1)請直接寫出C,D兩點的坐標.
(2)點P是線段BD上的一個動點,連接PC,PO,當點P在BD上移動時(不與B,D重合)![]() 的值是否發(fā)生變化?并說明理由.
的值是否發(fā)生變化?并說明理由.
(3)在坐標軸上是否存在一點M,使三角形MBC的面積與三角形ACD的面積相等?若存在直接寫出點M的坐標,若不存在,試說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某校舉行“做文明郴州人”演講比賽,聘請了10位評委為參賽選手打分,賽前,組委會擬定了四種記分方案:方案一:取所有評委所給的平均分;
方案二:在所有評委給的分中,去掉一個最高分,去掉一個最低分,取剩余得分的平均分;
方案三:取所有評委給分的中位數(shù);
方案四:取所有評委給分的眾數(shù).
為了探究四種記分方案的合理性,先讓一名表演選手(不參加正式比賽的)演講,讓10位評委給演講者評分,表演者得分如下表:
評委編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
打分 | 7.0 | 7.8 | 3.2 | 8.0 | 8.4 | 8.4 | 9.8 | 8.0 | 8.4 | 8.0 |
(1)請分別用上述四種方案計算表演者的得分;
(2)如果你是評委會成員,你會建議采用哪種可行的記分方案?你覺得哪幾種方案不合適?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】為了讓同學們了解自己的體育水平,初二1班的體育劉老師對全班45名學生進行了一次體育模擬測試(得分均為整數(shù)),成績滿分為10分,1班的體育委員根據(jù)這次測試成績,制作了統(tǒng)計圖和分析表如下:
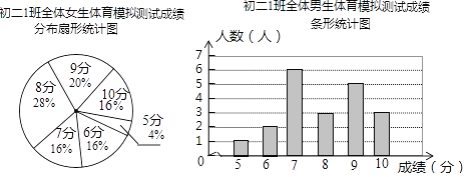
初二1班體育模擬測試成績分析表
平均分 | 方差 | 中位數(shù) | 眾數(shù) | |
男生 | 2 | 8 | 7 | |
女生 | 7.92 | 1.99 | 8 |
根據(jù)以上信息,解答下列問題:
(1)這個班共有男生________人,共有女生________人;
(2)補全初二1班體育模擬測試成績分析表.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,∠ABC=∠ACB,AD、BD、CD分別平分△ABC的外角∠EAC、內(nèi)角∠ABC、外角∠ACF.以下結(jié)論:
①AD∥BC;
②∠ACB=2∠ADB;
③∠ADC=90°﹣∠ABD;
④BD平分∠ADC;
⑤∠BDC=![]() ∠BAC.
∠BAC.
其中正確的結(jié)論有( )

A.2個 B.3個 C.4個 D.5個
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com