
【題目】如圖,在平面直角坐標(biāo)系中,矩形AOBC的邊長為AO=6,AC=8,
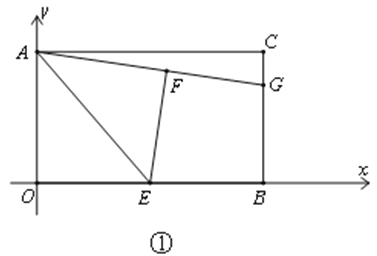
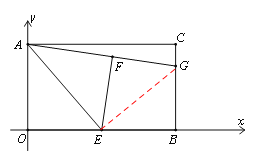
(1)如圖①,E是OB的中點,將△AOE沿AE折疊后得到△AFE,點F在矩形AOBC內(nèi)部,延長AF交BC于點G.求點G的坐標(biāo);
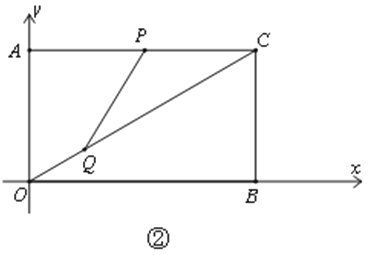
(2)定義:若以不在同一直線上的三點中的一點為圓心的圓恰好過另外兩個點,這樣的圓叫做黃金圓.如圖②,動點P以每秒2個單位的速度由點C向點A沿線段CA運動,同時點Q以每秒4個單位的速度由點O向點C沿線段OC運動;求:當(dāng) PQC三點恰好構(gòu)成黃金圓時點P的坐標(biāo).
【答案】(1)(8,![]() );(2)
);(2)![]() ,
,![]() ,
,![]() .
.
【解析】
試題(1)由折疊對稱的性質(zhì)可得DAOE≌DAFE,從而推出DEFG≌DEBG,得到DAOE∽DAEG,因此AE2=AO×AG,在Rt△AOE中,由勾股定理可得AE2=36+16=52,從而得AG=![]() ,在Rt△ABM中,由勾股定理可得CG=
,在Rt△ABM中,由勾股定理可得CG=![]() ,從而BG=
,從而BG=![]() ,得到G的坐標(biāo)為(8,
,得到G的坐標(biāo)為(8,![]() );(2)分點C為黃金圓的圓心,點P為黃金圓的圓心,點Q為黃金圓的圓心三種情況討論即可.
);(2)分點C為黃金圓的圓心,點P為黃金圓的圓心,點Q為黃金圓的圓心三種情況討論即可.
試題解析:(1)如圖,連接EG,
由題意得:DAOE≌DAFE,∴EFG=OBC=900.
又∵E是OB的中點,∴EG=EG,EF=EB=4.∴DEFG≌DEBG.
∴FEG=BEG,AOB=AEG=900. ∴DAOE∽DAEG,AE2=AO×AG.
又在Rt△AOE中,∵AO=6,OE=4,∴AE2=36+16=52.
∴52=6×AG,AG=![]() .
.
在Rt△ABM中,由勾股定理可得CG=![]() ,∴BG=
,∴BG=![]() .
.
∴G的坐標(biāo)為(8,![]() ) .
) .
(2)設(shè)運動的時間為t秒,
當(dāng)點C為黃金圓的圓心時,則CQ=CP,
即:2t=10—4t,得到t=![]() ,此時CP=
,此時CP=![]() ,AP=
,AP=![]() ,P點坐標(biāo)為
,P點坐標(biāo)為![]() .
.
當(dāng)點P為黃金圓的圓心時,則PC=PQ,
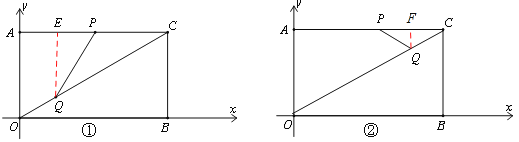
如圖①,過點Q作AC的垂線交AC于點E,CQ=10—4t,CP=2t.
由三角形相似可知:EQ=![]() CQ=
CQ=![]() ,PE=
,PE=![]() ,
,
則![]() ,
,![]() 化簡得:
化簡得:![]() ,
,
解得![]() (舍去).
(舍去).
此時,AP=![]() ,P點坐標(biāo)為
,P點坐標(biāo)為![]() .
.
當(dāng)點Q為黃金圓的圓心時,則QC=PQ,
如圖②,過點Q作AC的垂線交AC于點F,CQ=10—4t,CP=2t.
由三角形相似可知:QF=![]() ,PF=
,PF=![]() ,
,
則![]() ,整理得
,整理得![]() .
.
解得![]() (舍去).
(舍去).
此時,AP=![]() ,P點坐標(biāo)為
,P點坐標(biāo)為![]() .
.
綜上所述,P點坐標(biāo)為![]() ,
,![]() ,
,![]() .
.


科目:初中數(shù)學(xué) 來源: 題型:
【題目】師徒二人各加工同樣多的零件,師父每小時加工200個,徒弟每小時加工125個.若徒弟先加工段時間之后,師父才開始工作師父工作2小時后發(fā)現(xiàn)自己加工的零件個數(shù)和徒弟加工的個數(shù)剛好相同,如圖是師徒兩人完成的零件個數(shù)之差y(個)與徒弟工作的時間x(小時)之間的函數(shù)圖象,根據(jù)圖象回答問題:
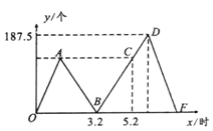
(1)求出點A的坐標(biāo),并解釋該點坐標(biāo)表示的實際意義;
(2)求出線段BD的函數(shù)表達(dá)式;
(3)求徒弟這次加工的零件總數(shù)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知MB=ND,∠MBA=∠NDC,下列哪個條件不能判定△ABM≌△CDN( )

A.AM=CNB.AB=CD C.AM∥CN D.∠M=∠N
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】請閱讀下列材料:
我們知道,分式類比分?jǐn)?shù),分?jǐn)?shù)中有真分?jǐn)?shù)、假分?jǐn)?shù)、帶分?jǐn)?shù)、類似的,在分式中,也規(guī)定真分式、假分式、帶分式;在分子、分母都是整式的情況下,如果分子的次數(shù)低于分母的次數(shù),稱這樣的分式為真分式.例如,分式![]() ,
,![]() 是假分式,一個假分式可以化為帶分式,即化為一個整式與一個真分式的和,例如,
是假分式,一個假分式可以化為帶分式,即化為一個整式與一個真分式的和,例如,![]() .(注意帶分式中整式與真分式之間的符號不能省略)
.(注意帶分式中整式與真分式之間的符號不能省略)
請根據(jù)以上方法,解決下列問題;
(1)請根據(jù)以上信息,任寫一個真分式 .
(2)已知:![]() ;
;
①當(dāng)![]() 時,若
時,若![]() 與
與![]() 都為正整數(shù),求
都為正整數(shù),求![]() 的值;
的值;
②計算![]() ,設(shè)
,設(shè)![]() ,探索
,探索![]() 是否有最小值,若有,請求出
是否有最小值,若有,請求出![]() 的值;若沒有,請說明理由.
的值;若沒有,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,正方形ABCD的邊長為1,點A與原點重合,點B在y軸的正半軸上,點D在x軸的負(fù)半軸上,將正方形ABCD繞點A逆時針旋轉(zhuǎn)30°至正方形AB'C′D′的位置,B'C′與CD相交于點M,則點M的坐標(biāo)為_____.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(9分)某批發(fā)商以每件50元的價格購進(jìn)800件T恤,第一個月以單價80元銷售,售出了200件;第二個月如果單價不變,預(yù)計仍可售出200件,批發(fā)商為增加銷售量,決定降價銷售,根據(jù)市場調(diào)查,單價每降低1元,可多售出10件,但最低單價應(yīng)高于購進(jìn)的價格;第二個月結(jié)束后,批發(fā)商將對剩余的T恤一次性清倉銷售,清倉是單價為40元,設(shè)第二個月單價降低![]() 元.
元.
(1)填表:(不需化簡)

(2)如果批發(fā)商希望通過銷售這批T恤獲利9000元,那么第二個月的單價應(yīng)是多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】若一個三角形一條邊的平方等于另兩條邊的乘積,我們把這個三角形叫做比例三角形.

![]() 已知
已知![]() 是比例三角形,
是比例三角形,![]() ,
,![]() ,請直接寫出所有滿足條件的AC的長;
,請直接寫出所有滿足條件的AC的長;
![]() 如圖1,在四邊形ABCD中,
如圖1,在四邊形ABCD中,![]() ,對角線BD平分
,對角線BD平分![]() ,
,![]() 求證:
求證:![]() 是比例三角形.
是比例三角形.
![]() 如圖2,在
如圖2,在![]() 的條件下,當(dāng)
的條件下,當(dāng)![]() 時,求
時,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,點
,點![]() 分別是
分別是![]() 的邊
的邊![]() 、
、![]() 的中點,邊
的中點,邊![]() 分別與
分別與![]() 、
、![]() 相交于點
相交于點![]() ,且
,且![]() ,連接
,連接![]() 、
、![]() 、
、![]() ,現(xiàn)在下列四個結(jié)論:
,現(xiàn)在下列四個結(jié)論:
①![]() ,②
,②![]() 平分
平分![]() ,③
,③![]() ,④
,④![]() .
.
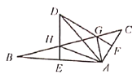
則其中正確的結(jié)論有( ).
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】王明同學(xué)隨機(jī)抽查某市![]() 個小區(qū)所得到的綠化率情況,結(jié)果如下表:
個小區(qū)所得到的綠化率情況,結(jié)果如下表:
小區(qū)綠化率 |
|
|
|
|
小區(qū)個數(shù) |
|
|
|
|
則關(guān)于這![]() 個小區(qū)的綠化率情況,下列說法錯誤的是( )
個小區(qū)的綠化率情況,下列說法錯誤的是( )
A. 極差是13% B. 眾數(shù)是25% C. 中位數(shù)是25% D. 平均數(shù)是26.2%
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com