
如圖,平面直角坐標系中,直線AB與![]() 軸,
軸,![]() 軸分別交于A(3,0),B(0,
軸分別交于A(3,0),B(0,![]() )兩點, ,點C為線段AB上的一動點,過點C作CD⊥
)兩點, ,點C為線段AB上的一動點,過點C作CD⊥![]() 軸于點D.
軸于點D.
(1)求直線AB的解析式;
(2)若S梯形OBCD=![]() ,求點C的坐標;
,求點C的坐標;
(3)在第一象限內是否存在點P,使得以P,O,B為頂點的
三角形與△OBA相似.若存在,請求出所有符合條件
的點P的坐標;若不存在,請說明理由.(做出一種答案即可)

(1)直線AB解析式為:y=![]() x+
x+![]() .
.
(2)方法一:設點C坐標為(x,![]() x+
x+![]() ),那么OD=x,CD=
),那么OD=x,CD=![]() x+
x+![]() .
.
∴![]() =
=![]() =
=![]() .
.
由題意:![]() =
=![]() ,解得
,解得![]() (舍去)
(舍去)
∴ C(2,![]() )
)
方法二:∵ ![]() ,
,![]() =
=![]() ,∴
,∴![]() .
.
由OA=![]() OB,得∠BAO=30°,AD=
OB,得∠BAO=30°,AD=![]() CD.
CD.
∴ ![]() =
=![]() CD×AD=
CD×AD=![]() =
=![]() .可得CD=
.可得CD=![]() .
.
 ∴ AD=1,OD=2.∴C(2,
∴ AD=1,OD=2.∴C(2,![]() ).
).
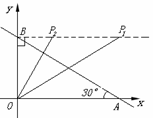
(3)當∠OBP=Rt∠時,如圖
①若△BOP∽△OBA,則∠BOP=∠BAO=30°,BP=![]() OB=3,
OB=3,
∴![]() (3,
(3,![]() ).
).
②若△BPO∽△OBA,則∠BPO=∠BAO=30°,OP=![]() OB=1.
OB=1.
∴![]() (1,
(1,![]() ).
).
當∠OPB=Rt∠時
③ 過點P作OP⊥BC于點P(如圖),此時△PBO∽△OBA,∠BOP=∠BAO=30°
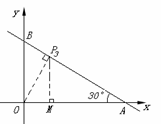 過點P作PM⊥OA于點M.
過點P作PM⊥OA于點M.
方法一: 在Rt△PBO中,BP=![]() OB=
OB=![]() ,OP=
,OP=![]() BP=
BP=![]() .
.
∵ 在Rt△PMO中,∠OPM=30°,
∴ OM=![]() OP=
OP=![]() ;PM=
;PM=![]() OM=
OM=![]() .∴
.∴![]() (
(![]() ,
,![]() ).
).
 方法二:設P(x ,
方法二:設P(x ,![]() x+
x+![]() ),得OM=x ,PM=
),得OM=x ,PM=![]() x+
x+![]()
由∠BOP=∠BAO,得∠POM=∠ABO.
∵tan∠POM==![]() =
=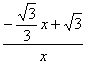 ,tan∠ABOC=
,tan∠ABOC=![]() =
=![]() .
.
∴![]() x+
x+![]() =
=![]() x,解得x=
x,解得x=![]() .此時,
.此時,![]() (
(![]() ,
,![]() ).
).
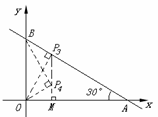
④若△POB∽△OBA(如圖),則∠OBP=∠BAO=30°,∠POM=30°.
∴ PM=![]() OM=
OM=![]() .
.
∴ ![]() (
(![]() ,
,![]() )(由對稱性也可得到點
)(由對稱性也可得到點![]() 的坐標).
的坐標).
當∠OPB=Rt∠時,點P在x軸上,不符合要求.
綜合得,符合條件的點有四個,分別是:
![]() (3,
(3,![]() ),
),![]() (1,
(1,![]() ),
),![]() (
(![]() ,
,![]() ),
),![]() (
(![]() ,
,![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
 11、象棋中的馬走日字對角(如圖1由點A到點B或由點A到點C),現建立如圖2平面直角坐標系,則下一步可能到達的點的坐標是
11、象棋中的馬走日字對角(如圖1由點A到點B或由點A到點C),現建立如圖2平面直角坐標系,則下一步可能到達的點的坐標是查看答案和解析>>
科目:初中數學 來源: 題型:
| k | x |
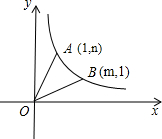 OA、OB.
OA、OB.查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖平面直角坐標系中,已知點A的坐標為(-3,-1),點B的坐標為(2,-4).
如圖平面直角坐標系中,已知點A的坐標為(-3,-1),點B的坐標為(2,-4).查看答案和解析>>
科目:初中數學 來源: 題型:
 在如圖平面直角坐標系中,△ABC三個頂點A、B、C的坐標分別為A(2,-1),B(1,-3),C(4,-4),
在如圖平面直角坐標系中,△ABC三個頂點A、B、C的坐標分別為A(2,-1),B(1,-3),C(4,-4),查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com