
【題目】如圖,已知反比例函數![]() 的圖像與一次函數
的圖像與一次函數![]() 的圖象相交于點A(1,4)和點B(m,-2).
的圖象相交于點A(1,4)和點B(m,-2).
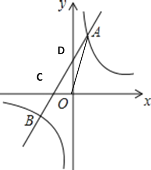
(1)求反比例函數和一次函數的解析式;
(2)求ΔAOC的面積;
(3)直接寫出![]() 時的x的取值范圍 (只寫答案)
時的x的取值范圍 (只寫答案)
【答案】(1)![]() ,
,![]() ;(2)C(-3,0), S=6;(3)
;(2)C(-3,0), S=6;(3)![]() 或
或![]()
【解析】
(1)根據題意把A的坐標代入反比例函數![]() 的圖像與一次函數
的圖像與一次函數![]() ,分別求出k和b,從而即可確定反比例函數和一次函數的解析式;
,分別求出k和b,從而即可確定反比例函數和一次函數的解析式;
(2)由題意先求出C的坐標,再利用三角形面積公式求出ΔAOC的面積;
(3)根據函數的圖象即可得出一次函數的值大于反比例函數的值的x的取值范圍.
解:(1)將點A(1,4)代入反比例函數![]() 的圖像與一次函數
的圖像與一次函數![]() ,求得
,求得![]() 以及
以及![]() ,
,
所以反比例函數和一次函數的解析式分別為:![]() 和
和![]() ;
;
(2)因為C在一次函數![]() 的圖象上以及x軸上,所以求得C坐標為(-3,0),
的圖象上以及x軸上,所以求得C坐標為(-3,0),
則有OC=3, ΔAOC以OC為底的高為4,所以ΔAOC的面積為:![]() ;
;
(3)由![]() 可知一次函數的值大于反比例函數的值,
可知一次函數的值大于反比例函數的值,
把B(m,-2)代入![]() ,得出m=-2,即B(-2,-2),
,得出m=-2,即B(-2,-2),
此時當![]() 或
或![]() 時,一次函數的值大于反比例函數的值.
時,一次函數的值大于反比例函數的值.


 初中暑期銜接系列答案
初中暑期銜接系列答案科目:初中數學 來源: 題型:
【題目】地下停車場的設計大大緩解了住宅小區停車難的問題,如圖是龍泉某小區的地下停車庫坡道入口的設計示意圖,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5m.根據規定,地下停車庫坡道入口上方要張貼限高標志,以便告知駕駛員所駕車輛能否安全駛入.小剛認為CD的長就是所限制的高度,而小亮認為應該以CE的長作為限制的高度.小剛和小亮誰說得對?請你判斷并計算出正確的限制高度.(結果精確到0.1m,參考數據:sin18°≈0.31,cos18°≈0.95,tan18°≈0.325)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,曲線AB是頂點為B,與y軸交于點A的拋物線y=﹣x2+4x+2的一部分,曲線BC是雙曲線y=![]() 的一部分,由點C開始不斷重復“A﹣B﹣C”的過程,形成一組波浪線,點P(2018,m)與Q(2025,n)均在該波浪線上,則
的一部分,由點C開始不斷重復“A﹣B﹣C”的過程,形成一組波浪線,點P(2018,m)與Q(2025,n)均在該波浪線上,則![]() =___________.
=___________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線![]() 經過
經過![]() 的三個頂點,其中點
的三個頂點,其中點![]() ,點
,點![]() ,
,![]() 軸,點
軸,點![]() 是直線
是直線![]() 下方拋物線上的動點.
下方拋物線上的動點.
(1)求拋物線的解析式;
(2)過點![]() 且與
且與![]() 軸平行的直線
軸平行的直線![]() 與直線
與直線![]() 、
、![]() 分別交與點
分別交與點![]() 、
、![]() ,當四邊形
,當四邊形![]() 的面積最大時,求點
的面積最大時,求點![]() 的坐標;
的坐標;
(3)當點![]() 為拋物線的頂點時,在直線
為拋物線的頂點時,在直線![]() 上是否存在點
上是否存在點![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 為頂點的三角形與
為頂點的三角形與![]() 相似,若存在,直接寫出點
相似,若存在,直接寫出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
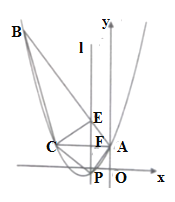
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,拋物線y=ax2+bx+c與x軸交于A(-1,0),B(3,0)兩點,與y軸交于點C. 點D(2,3)在該拋物線上,直線AD與y軸相交于點E,點F是直線AD上方的拋物線上的動點.
(1)求該拋物線對應的二次函數關系式;
(2)當點F到直線AD距離最大時,求點F的坐標;
(3)如圖2,點M是拋物線的頂點,點P的坐標為(0,n),點Q是坐標平面內一點,以A,M,P,Q為頂點的四邊形是AM為邊的矩形.①求n的值;②若點T和點Q關于AM所在直線對稱,求點T的坐標.
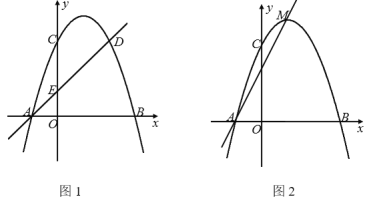
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,點P,D分別是BC,AC邊上的點,且∠APD=∠B.
(1)求證:△ABP∽△PCD;
(2)若AB=10,BC=12,當PD∥AB時,求BP的長.
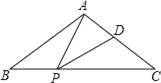
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線![]() 經過
經過![]() ,
,![]() 兩點,與x軸的另一個交點為C,頂點為D,連結CD.
兩點,與x軸的另一個交點為C,頂點為D,連結CD.
(1)求該拋物線的表達式;
(2)點P為該拋物線上一動點(與點B、C不重合),設點P的橫坐標為t.
①當點P在直線BC的下方運動時,求![]() 的面積的最大值;
的面積的最大值;
②該拋物線上是否存在點P,使得![]() 若存在,求出所有點P的坐標;若不存在,請說明理由.
若存在,求出所有點P的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是小明同學設計的“過圓外一點作圓的切線”的尺規作圖的過程.
已知:如圖1,![]() 和
和![]() 外的一點
外的一點![]() .
.

求作:過點![]() 作
作![]() 的切線.
的切線.
作法:如圖2,
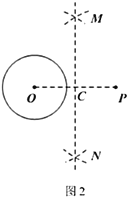
①連接![]() ;
;
②作線段![]() 的垂直平分線
的垂直平分線![]() ,直線
,直線![]() 交
交![]() 于
于![]() ;
;
③以點![]() 為圓心,
為圓心,![]() 為半徑作圓,交
為半徑作圓,交![]() 于點
于點![]() 和
和![]() ;
;
④作直線![]() 和
和![]() .
.
則![]() ,
,![]() 就是所求作的
就是所求作的![]() 的切線.
的切線.
根據上述作圖過程,回答問題:
(1)用直尺和圓規,補全圖2中的圖形;
(2)完成下面的證明:
證明:連接![]() ,
,![]() ,
,
∵由作圖可知![]() 是
是![]() 的直徑,
的直徑,
∴![]() (______)(填依據),
(______)(填依據),
∴![]() ,
,![]() ,
,
又∵![]() 和
和![]() 是
是![]() 的半徑,
的半徑,
∴![]() ,
,![]() 就是
就是![]() 的切線(______)(填依據).
的切線(______)(填依據).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com