
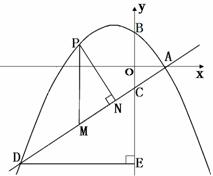
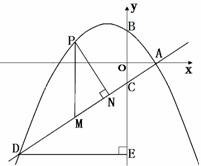
如圖,拋物線![]() 與x軸交于點A(2,0),交y軸于點B(0,
與x軸交于點A(2,0),交y軸于點B(0,![]() )直線y=kx
)直線y=kx![]() 過點A與y軸交于點C與拋物線的另一個交點是D。
過點A與y軸交于點C與拋物線的另一個交點是D。
⑴求拋物線![]() 與直線y=kx
與直線y=kx![]() 的解析式;
的解析式;
⑵設(shè)點P是直線AD上方的拋物線上一動點(不與點A、D重合),過點P作 y軸的平行線,交直線AD于點M,作DE⊥y軸于點E.探究:是否存在這樣的點P,使四邊形PMEC是平行四邊形,若存在請求出點P的坐標(biāo),若不存在,請說明理由;
⑶在⑵的條件下,作PN⊥AD于點N,設(shè)△PMN的周長為![]() ,點P的橫坐標(biāo)為x,求
,點P的橫坐標(biāo)為x,求![]() 與x的函數(shù)關(guān)系式,并求出
與x的函數(shù)關(guān)系式,并求出![]() 的最大值.
的最大值.
解:⑴∵![]() 經(jīng)過點A(2,0)和B(0,
經(jīng)過點A(2,0)和B(0,![]() )
)
∴由此得: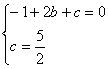 解得:
解得: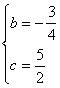
∴拋物線的解析式是![]() ∵直線y=kx
∵直線y=kx![]() 經(jīng)過點A(2,0)
經(jīng)過點A(2,0)
∴2k![]() =0 解得:k=
=0 解得:k=![]()
∴直線的解析式是![]()
⑵設(shè)P的坐標(biāo)是(![]() ),則M的坐標(biāo)是(x,
),則M的坐標(biāo)是(x,![]() )
)
∴PM=(![]() )-(
)-(![]() )=
)=![]() ……4分
……4分
解方程組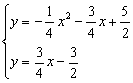 解得:
解得:
![]()
∵點D在第三象限,則點D的坐標(biāo)是(-8,![]() )
)
由![]() 得點C的坐標(biāo)是(0,
得點C的坐標(biāo)是(0,![]() )
)
∴CE=![]() -(
-(![]() )=6 由于PM∥y軸,要使四邊形PMEC是平行四邊形,必有PM=CE,
)=6 由于PM∥y軸,要使四邊形PMEC是平行四邊形,必有PM=CE,
即![]() =6
=6
解這個方程得:x1=-2,x2=-4 符合-8<x<2
當(dāng)x1=-2時,![]()
當(dāng)x1=-4時,![]()
因此,直線AD上方的拋物線上存在這樣的點P,使四邊形PMEC是平行四邊形,點P的坐標(biāo)是(-2,3)和(-4,![]() )
)
⑶在Rt△CDE中,DE=8,CE=6
由勾股定理得:DC=![]()
∴△CDE的周長是24
∵PM∥y軸,容易證明△PMN∽△CDE
∴![]() , 即
, 即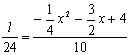
化簡整理得:![]() 與x的函數(shù)關(guān)系式是:
與x的函數(shù)關(guān)系式是:![]()
![]()
∵![]() ,∴
,∴![]() 有最大值
有最大值
當(dāng)x=-3時,![]() 的最大值是15
的最大值是15


 探究與鞏固河南科學(xué)技術(shù)出版社系列答案
探究與鞏固河南科學(xué)技術(shù)出版社系列答案科目:初中數(shù)學(xué) 來源: 題型:
 如圖,拋物線與x軸交于A(-1,0)、B(3,0)兩點,與y軸交于點C(0,-3),設(shè)拋物線的頂點為D.
如圖,拋物線與x軸交于A(-1,0)、B(3,0)兩點,與y軸交于點C(0,-3),設(shè)拋物線的頂點為D.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
 如圖,拋物線與x軸交于A(x1,0)、B(x2,0)兩點,且x1<x2,與y軸交于點C(0,-4),其中x1,x2是方程x2-4x-12=0的兩個根.
如圖,拋物線與x軸交于A(x1,0)、B(x2,0)兩點,且x1<x2,與y軸交于點C(0,-4),其中x1,x2是方程x2-4x-12=0的兩個根.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
 (2012•歷下區(qū)一模)如圖,拋物線與x軸交于A(-1,0),B(4,0)兩點,與y軸交于C(0,3),M是拋物線對稱軸上的任意一點,則△AMC的周長最小值是
(2012•歷下區(qū)一模)如圖,拋物線與x軸交于A(-1,0),B(4,0)兩點,與y軸交于C(0,3),M是拋物線對稱軸上的任意一點,則△AMC的周長最小值是| 10 |
| 10 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
 如圖,拋物線與y軸交于點A(0,4),與x軸交于B、C兩點.其中OB、OC是方程的x2-10x+16=0兩根,且OB<OC.
如圖,拋物線與y軸交于點A(0,4),與x軸交于B、C兩點.其中OB、OC是方程的x2-10x+16=0兩根,且OB<OC.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
 如圖,拋物線與x軸交于A、B(6,0)兩點,且對稱軸為直線x=2,與y軸交于點C(0,-4).
如圖,拋物線與x軸交于A、B(6,0)兩點,且對稱軸為直線x=2,與y軸交于點C(0,-4).查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com